728x90
반응형
출처 : https://book.naver.com/bookdb/book_detail.nhn?bid=21488029
공개적 빅데이터분석기사 실기
본 도서는 한국데이터산업진흥원에서 실시하는 빅데이터분석기사 국가기술자격 실기시험 대비 도서입니다.본 교재는 PYTHON을 활용하여 쉽고 빠른 자격증 취득으로 이어질 수 있도록 도움을 줄
book.naver.com
*해당 글은 학습을 목적으로 위의 도서 내용 중 일부 내용만을 요약하여 작성한 포스팅입니다.
상세 내용 및 전체 내용 확인을 원하신다면 도서 구매를 추천드립니다.
군집분석
- 군집분석은 개체들의 특성을 대표하는 몇 개의 변수들을 기준으로 몇 개의 그룹(군집)으로 세분화하는 방법이다.
- 즉 개체들을 여러 변수들을 기준으로 다차원 공간에서 유사한 특성을 가진 개체로 묶는 방법이다.
- 개체들 간의 유사성은 개체 간 거리를 이용하고, 거리가 상대적으로 가까운 개체들을 동일 군집으로 묶는다. 그리고 이 때 거리는 행렬을 이용하여 계산하는데, 대표적인 방법으로는 유클리디안 거리가 있다.
- sklearn.clustering 내에 있는 KMeans를 사용하여 구현한다.
- 주요 파라미터는 n_cluster로 군집의 수를 의미한다.
- 먼저 데이터를 로드한다.
import pandas as pd
from sklearn.preprocessing import MinMaxScaler
from sklearn.model_selection import train_test_split
from sklearn.cluster import KMeans
import warnings
warnings.filterwarnings('ignore')
data = pd.read_csv('/Mall_Customers.csv', encoding='utf-8')
# Income, Spend만 사용
# 두 데이터의 단위가 같기에 전처리는 불필요
x = data[data.columns[3:5]]- 그 후에는 최적 군집수를 찾아야 한다.
- KMeans 모델의 inerita_ 값을 살펴보면 되는데, 이는 군집과 각 개체간 거리를 계산하며 중심과 개체간 거리가 작아진다는 것은 군집이 잘 형성되었다는 것을 의미하다.
- 물론 무조건 작은 것만이 좋은 것은 아니고, 크게 감소하다가 변화가 없는 지점에서 최적의 군집수를 결정한다.
import matplotlib.pyplot as plt
wcss = []
for i in range(1, 21) :
kmeans = KMeans(n_clusters=i)
kmeans.fit_transform(x)
wcss.append(kmeans.inertia_)
plt.figure()
plt.plot(range(1, 21), wcss)
plt.title('The Elbow Method')
plt.xlabel('Number of clusters')
plt.ylabel('WCSS')
plt.show()
- 위의 결과로는 5가 제일 적당해 보이므로 5를 군집수로 선정하여 학습한 후 결과를 출력해본다.
k = 5
model = KMeans(n_clusters=k)
model.fit(x)
pred_y = model.predict(x)
# 저장
pred_y_pd = pd.DataFrame(pred_y)
pred_y_pd.columns = ['Group']
result_data = pd.concat([data, pred_y_pd], axis=1)
result_data.to_csv('/result_data.csv')
# 그래프에 출력
import numpy as np
import matplotlib.cm
labels = [('Cluster' + str(i+1)) for i in range(k)]
cmap = matplotlib.cm.get_cmap('plasma')
x = np.array(x)
plt.figure()
for i in range(k) :
plt.scatter(x[pred_y == i, 0], x[pred_y == i, 1], s = 20, c = cmap(i/k), label = labels[i])
plt.show()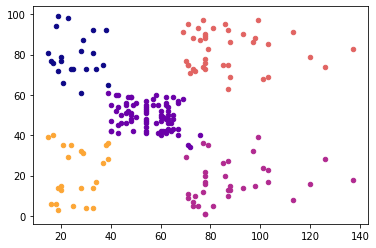
- 만약 중심점도 함께 찍어보고 싶다면 아래와 같은 코드를 추가하면 된다.
plt.scatter(model.cluster_centers_[:, 0],
model.cluster_centers_[:, 1],
s = 100,
c = 'black',
label = 'Centroids',
marker = 'X')
- k-means는 비계층적 군집 분석으로, 분석속도가 빠르고 군집을 형성하는 과정에서 유연하게 다른 군집으로 재군집화가 가능한 방법이다.
- 계층적 군집 분석이란 방법도 있는데, 한 번 어떤 군집에 속한 개체는 분석 과정에서 다른 군집과 더 가깝게 계산되어도 재군집화가 이루어지지 않는 방법으로, 속도가 다소 오래 걸린다.
import pandas as pd
import numpy as np
from sklearn.preprocessing import MinMaxScaler
from sklearn.model_selection import train_test_split
from sklearn.cluster import KMeans
import warnings
import matplotlib.cm as cm
import matplotlib.pyplot as plt
cmap = cm.get_cmap('plasma')
warnings.filterwarnings('ignore')
data = pd.read_csv('/Mall_Customers.csv', encoding='utf-8')
# Income, Spend만 사용
x = data[data.columns[3:5]]
# 군집이 형성되는 과정 파악
import scipy.cluster.hierarchy as sch
plt.figure(1)
z = sch.linkage(x, method = 'ward')
dendrogram = sch.dendrogram(z)
plt.title("Dendrogram")
plt.xlabel('Customers')
plt.ylabel('ward distances')
plt.show()
- 다음으로 군집수를 5로 하여 병합 군집을 적용한 군집분석을 수행한다.
- 이 방법은 각 포인트를 하나의 클러스터로 지정하고 그 다음 종료 조건 (지정한 군집 수)를 만족할 때까지 가장 비슷한 두 클러스터를 합치는 방식으로 진행한다.
k = 5
from sklearn.cluster import AgglomerativeClustering
model = AgglomerativeClustering(n_clusters = k, affinity = 'euclidean', linkage='ward')
pred_y = model.fit_predict(x)
labels = [('Cluster ' + str(i+1)) for i in range(k)]
x = x.values
plt.figure(2)
for i in range(k) :
plt.scatter(x[pred_y == i, 0], x[pred_y == i, 1], s = 20, c = cmap(i/k), label = labels[i])
plt.show()
DBSCAN
- DBSCAN은 밀도 기반 클러스터링 기법이다.
- 이 방법은 케이스가 집중된 밀도에 초점을 두고 밀도가 높은 그룹을 클러스터링 하는 방식이다.
- 중심점을 기준으로 특정한 반경 이내에 케이스가 n개 이상 있을 경우 하나의 군집을 선정한다.
- sklearn.cluster 내의 DBSCAN 라이브러리를 이용한다.
- 주요 파라미터는 eps, min_samples가 있다.
- eps는 엡실론으로, 근접 이웃점을 찾기 위해 정의 내려야 하는 반경 거리이다.
- min_samples는 하나의 군집을 형성하기 위해 필요한 최소 케이스 수이다.
import warnings
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.cluster import DBSCAN
data = pd.read_csv('/iris.csv')
x = data[data.columns[0:4]]
model = DBSCAN(eps = 0.5, metric = 'euclidean', min_samples = 5)
model.fit(x)
print('군집 :', np.unique(model.labels_))
pred_y = model.fit_predict(x)
# 결과 저장
pred_y = pd.DataFrame(pred_y)
pred_y.columns = ['predict']
result_data = pd.concat([data, pred_y], axis = 1)
result_data.to_csv('/result_iris.csv')
# 실 데이터와 예측 데이터 교차표 확인
print(pd.crosstab(result_data['class'], result_data['predict']))
# 시각화
# 변수가 네 개이므로 4차원에 표현해야 하지만 현실적으로 불가능하므로
# PCA를 통해 2차원에 표현
from sklearn.decomposition import PCA
pca = PCA(n_components=2).fit(x)
pca_2d = pca.transform(x)
for i in range(0, pca_2d.shape[0]) :
if model.labels_[i] == 0 :
c1 = plt.scatter(pca_2d[i, 0], pca_2d[i, 1], c = 'r', marker = '+')
elif model.labels_[i] == 1 :
c2 = plt.scatter(pca_2d[i, 0], pca_2d[i, 1], c = 'g', marker = 'o')
elif model.labels_[i] == -1 :
c3 = plt.scatter(pca_2d[i, 0], pca_2d[i, 1], c = 'b', marker = '*')
plt.legend([c1, c2, c3], ['Cluster1', 'Cluster2', 'Noise'])
plt.title('DBSCAN')
plt.show()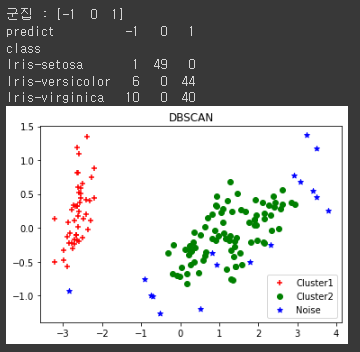
728x90
반응형
'자격증 > 빅데이터 분석기사 (실기)' 카테고리의 다른 글
| 04. 머신러닝 핵심 알고리즘 (3) (0) | 2022.06.07 |
|---|---|
| 04. 머신러닝 핵심 알고리즘 (2) (0) | 2022.06.06 |
| 04. 머신러닝 핵심 알고리즘 (1) (0) | 2022.06.05 |
| 03_03. 머신러닝 프로세스 (0) | 2022.06.04 |
| 03_02. 회귀 (0) | 2022.06.04 |


