- 강의 목록
- Optimization (최적화)
- CNN 첫걸음
- 요약
강의
뉴럴 네트워크의 최적화와 관련해 일반화 성능, 교차 검증, 경사 하강법, 정규화 등을 학습했다.
CNN의 개념 중 콘볼루션 연산에 대해 학습했다.
피어세션
어제의 내용을 복습하는 시간을 가졌고, 과제 코드를 함께 분석하는 시간을 가졌다.
- 학습정리
Optimization (최적화)
Generalization (일반화 성능)

- 학습한 적 없는 데이터에서 얼마나 잘 작동하는지 테스트 한 것.
- 일반화 성능은 학습 에러와 테스트 에러의 차이가 크지 않음을 의미한다.
- 무작정 학습 에러가 적다고 좋은 것이 아니다.
Underfitting vs Overfitting

- Underfitting (과편향) : 모델이 너무 단순해서 데이터에 내제된 구조를 학습하지 못하는 것.
- Overfitting (과분산) : 모델이 훈련 데이터에 너무 잘 맞아 일반성이 떨어지는 것.
| 구분 | 원인 | 해결 |
| 오버피팅 | 학습 데이터 편중 | 다양한 훈련 데이터확보 |
| 과도한 양의 특징들 | 정규화, 표준화 | |
| 무분별한 Noise 수용 | Dropout | |
| 언더피팅 | 부적절한 분석 모형 | 분석 모델 유연성 확보 |
| 학습 데이터 부족 | 충분한 학습데이터 확보 | |
| 표준 집합 부족 | Cross Validation |
Cross Validation (교차검증)
- 학습데이터와 테스트데이터를 나누어 진행한다.
- 학습 데이터를 k개로 나누어 1개로 테스트, 나머지로 학습
- 매번 테스트 데이터를 달리해 k번의 학습을 반복한다.
- 특정 평가 데이터 셋에 오버피팅 되는 것을 방지할 수 있다.
- 학습 횟수가 많기 때문에 시간이 조금 오래 걸린다.
Bias and Variance

- Variance : 비슷한 입력에 대한 일관된 출력 정도 (작을수록 좋음)
- Bias : 같은 입력에 대해서 출력의 평균 정도 (작을수록 좋음)
- 학습데이터의 잡음을 최소화하는데, 하나를 올리면 하나가 내려감
- bias와 variance를 둘 다 줄이는 것은 힘들다
Bootstrapping

- 서브 샘플링으로 학습 데이터를 나누어 여러 모델을 만드는 것.
- 학습데이터 전체가 아니라 일부만 활용한 여러 모델을 만드는 것.
- 딱 하나의 단일 통계치가 아니라, 여러 모델을 만들어 평균을 구한다.
- 여러 모델의 일치도를 보기 위해 활용
- 데이터 셋 내의 데이터 분포가 고르지 않은 경우 사용된다.
- 데이터 셋의 분포가 고르지 않을 때 고르게 만들 수 있다.
Bagging (Bootstrapping aggregating)
- 학습데이터를 전부 사용하여 한 개의 모델을 만드는 게 아니라 나눠 여러 모델을 만든다
- 여러 모델의 아웃풋의 평균을 내기 위해 사용.
Boosting
- 시퀀셜하게 간단한 모델을 만들어서 돌려본다.
- 잘 안되는 데이터에 대해서만 모델을 추가로 만든다.
- 이렇게 만들어진 모델들을 시퀀셜하게 합쳐 하나의 모델을 만든다.
Gradient Descent (경사 하강법)
- 모델이 출력한 결과값과 실제값 사이의 차이인 Loss Function을 최소화 하기 위해 loss를 줄이는 방향으로 기울기를 업데이트 하는 것.
- 근데 일반적인 GD는 모든 데이터를 전부 넣어 기울기를 계산하기에 너무 느렸다.
- 그래서 나온 게 SGD이다.
1) Stochastic gradient descent (SGD)
- 데이터 셋에서 한 개의 샘플을 추출해 error gradient를 계산하고 gradient descent 알고리즘을 적용하는 방법.
- 상대적으로 빠르고, local optimal에 빠질 리스크가 적다.
- 데이터를 한 개씩 처리하기 때문에 메모리에 부담이 가고, global optimal을 찾지 못할 수 있다.
2) Mini-batch gradient descent :
- 데이터를 여러 미니배치로 나눠 한 개의 미니 배치마다 기울기를 구하고 모델을 업데이트.
- SGD보다 병렬처리가 좋다.
- 에러에 대한 정보를 미니배치 크기만큼 축적해 계산하기 때문에 SGD보다 메모리 사용이 높다.
3) Batch gradient descent :
- 전체 데이터 셋으로 에러를 구한 뒤 기울기를 한 번만 계산
- 전체 데이터에 대해 업데이트가 한 번에 이루어지기에 병렬 처리에 유리하고 global optimal로 수렴이 안정적이다.
- 학습이 오래걸리고 local optimal 상태가 되면 빠져나오기 힘들다.
*global optimal : loss 값이 최소에 도달하는 지점
*local optimal : loss 값이 최소가 아닌데 이후에 증가한다고 프로그램이 최소로 인식하는 구간.
*Batch size matter

-배치 사이즈가 크면 sharp minimizer에 도달한다.
-배치 사이즈가 작으면 flat minimizer에 도달한다.
*즉, 배치 사이즈가 작은게 더 좋다.
*flat minimizer은 트레이닝에서 잘 되면 테스팅에서도 잘 되기에 일반화 성능이 높다
*sharp minimum에서는 트레이닝에서 얻어지는 값들이 테스트 데이터에서는 제대로 동작 안함
경사 하강법 메소드
- 계산 자체는 프로그램이 알아서 해주지만 경사 하강법은 직접 골라야 한다.
1) SGD

- 전체가 아닌 조금만 훑어보고 일단 빨리 가는 것.
- learning rate를 잡는 것이 어렵다. 크거나 작으면 학습이 잘 안됨.
2) 모멘텀

- 모멘텀이 이전의 경사를 계속 들고있는 형태.
- 경사가 바뀔 때 이전의 경사 정보를 활용한다.
- 일종의 가속도 개념으로, 경사 방향이 변할 때 감소하던 혹은 증가하던 방향으로 더 많이 변화한다.
- 한 번 흘러가기 시작한 경사를 유지하여 경사가 계속 바뀌어도 학습이 잘 됨
3) Nesterov Accelerated Gradient (NAG)


- 모멘텀 방법에서 현재의 파라미터 부분에 대한 부분을 수정하여 목적 함수를 사용
- 모멘텀은 이동 벡터 VT를 계산할 때 현재 위치에서 GRADIENT와 MOMENTUM STEP을 독립적으로 계산하고 합친다.
- NAG는 MOMENT STEP을 먼저 고려해 MOMENTUM STEP을 먼저 이동했다고 생각한 후 그 자리에서 기울기를 구해 이동한다.
- 즉, 경사 계산시 LAG를 계산해 미리 한 번 이동한 다음 해당 위치의 경사를 누적한다.
4) Adagrad

- 뉴럴 네트워크의 파라미터의 변화 정도를 파악한다.
- 학습률이 너무 작으면 학습 시간이 너무 길고, 너무 크면 발산해서 학습이 제대로 이루어지지 않는 현상을 학습률 감소를 통해 해결한 것.
- 많이 변한 파라미터는 적게 변화시키고, 조금 변한 파라미터는 많이 변화시킨다.
- G에 파라미터의 변화 정도를 누적한다. (큰 값일수록 많이 변함)
- 근데 G가 계속 커져서 학습이 진행될수록 학습이 멈춘다. (변화를 안시킴, 학습률이 0이 됨.)
5) Adadelta

- G가 계속해서 커지는 현상을 막기 위해 합을 구하는 대신 지수 평균을 구한다.
- 현재 타임스탬프 T가 주어지면 시간에 대한 파라미터의 변화를 잡는다.
- 근데 G를 누적하는 것이 아니라 따로 두기에 학습이 진행될수록 G의 개수가 너무 많아진다.
- 익스탠셜 무빙 에버리지로 막는다.
*Adadelta에는 LEARNING RATE이 없어 개발자가 직접 변경할 수 있는 요소가 없다.
*Learning rate이 필요없는 이유는 H가 없데이트 하려는 가중치의 변화값을 들고있기 때문
*개발자가 직접 변경할 수 없어 잘 활용하지 않는다.
6) RMSprop

- AdaGrad에서 기울기의 누적으로 인해 학습률이 0이 되는 것을 방지.
- 기울기를 단순 누적하지 않고 지수 가중 이동 평균을 사용해 최신 기울기들이 더 크게 반영되도록 했다.
- stepsize를 넣어 기울기들의 최신 정도를 파악한다.
7) Adam

- 가장 무난하게 사용하는 함수
- 모멘텀과 AdaGrad를 융합한 방법.
- 그래디언트의 크기가 변함에 따라 이전의 그래디언트 정보를 합친다.
Regularization
- 일반화 성능을 잘 측정하기 위해 규제를 거는 것
- 학습을 방해함으로써 학습 데이터에만 잘 동작하는 오버피팅을 방지한다.
1) Early Stopping
- 각 EPOCH마다 성능을 측정하고, 좋은 성능이 나오면 멈춘다.
- 이 때 검증은 학습에 활용하지 않은 데이터 셋으로 해야 한다.
2) Parameter Norm Penalty

- 뉴럴 네트워크는 숫자들이 작아야 학습이 더 잘 진행된다.
- 뉴럴 네트워크의 파라미터가 너무 커지지 않게 하는 방법
- 비용함수에 제곱을 더하거나 절댓값을 더해서 웨이트의 크기에 제한을 준다.
*L2 weight decay (제곱값)
*L1 weight decay (절댓값)
3) Data Augmentation
- 한정된 데이터를 더 많은 데이터로 늘리는 방법
- 데이터를 자르거나, 미러링하거나, 회전하는 등으로 데이터의 수를 늘리는 것
4) Noise Robustness

- 입력 데이터에 노이즈를 집어넣어 노이즈가 있는 데이터에 익숙해지게 만든다.
- 단순히 데이터에만 하는 게 아니라 가중치에도 노이즈를 넣는다.
*Robust : 이상치나 노이즈가 들어와도 흔들리지 않고 잘 일반화 하는 것.
5) Label Smoothing

- 0과 1로 이루어진 레이블을 0~1 까지의 다양한 값으로 변화 ex) [0, 1, 0] => [0.025, 0.95, 0.025]
- 이진분류에서 모델이 둘 중 하나만 정확하게 예측하지 않게 만든다.
- 데이터 셋 자체는 사람이 만드는 것이기 때문에 실수의 가능성이 있고, 오분류된 데이터가 있을 수 있다.
- 이를 대비해 모델을 둘 중 하나만 정확하게 예측하게 만들지 말고, 유하게 학습시키면 효과적.
- 학습 데이터를 두 개를 뽑아서 섞어주는 방식으로 만든다.
- 노력 대비 성능 향상이 좋은 편.
6) Dropout

- 뉴런의 일부를 랜덤으로 꺼서 랜덤한 모델을 만든다.
7) Batch Normalization

- 뉴럴 네트워크는 기본적으로 숫자의 범위가 작아야 학습이 효율적으로 이루어진다.
- 하지만 여러 레이어를 거치면 레이어의 결과로 파라미터가 계속 변화한다.
- 더 나은 학습 효율을 위해서는 레이어의 결과로 나온 파라미터를 정규화해야 한다.
- 하지만 일반 정규화 (평균 0, 표준편차 1)로 정규화시 활성 함수의 비선형성이 사라진다.
- ex) sigmoid의 경우 (-1.96, 1.96)이 선형인데 이 부분에만 속할 수 있다.
- 그래서 전체가 아닌 배치 단위 별로 평균과 분산을 이용해 정규화 한다.

CNN
Convolution 연산



- 커널을 입력벡터 상에서 움직이며 선형모델과 합성함수가 적용되는 연산
- 커널을 이용해 정보를 국소적으로 확산, 추출, 감소하는 것.
- 커널은 정의역 내에서 움직여도 변하지 않고 주어진 신호에 국소적으로 적용한다.
- 1차원 뿐 아니라 다양한 차원에서의 연산도 가능하다.
- 데이터의 성격에 따라 사용하는 커널이 달라진다.
*커널 = 필터 = 가중치
2차원 Convolution 연산

- 2차원 연산은 커널을 입력벡터 상에서 움직여가며 선형모델과 합성함수가 적용된다.
- 입력 크기를 (H, W), 커널크기를 (KH,KW),출력크기를 (OH, OW)라 하면 출력크기는 다음과 같이 계산한다.
3차원 Convolution 연산
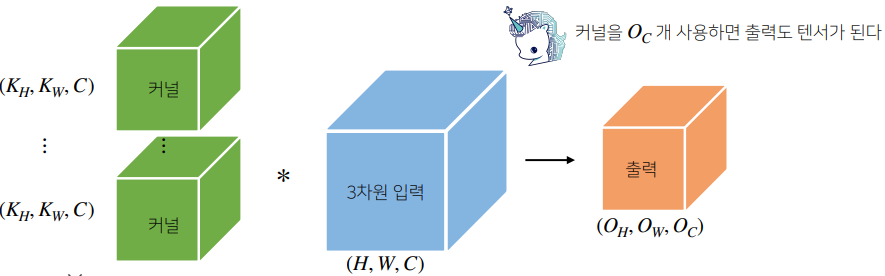

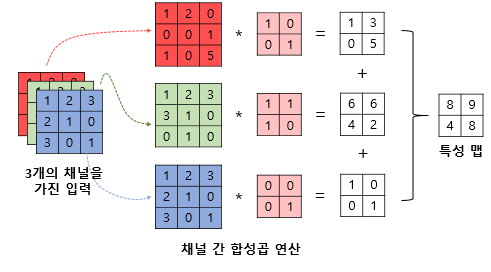
- 3차원 연산의 경우는 2차원 연산을 세 번 적용한다.
- 3차원 부터는 행렬이 아닌 텐서라 칭한다.
- 3차원 연산은 커널의 채널수와 입력의 채널수가 같아야 출력도 텐서가 된다.
Convolution 연산의 역전파

- 커널이 모든 입력데이터에 공통으로 적용되기에 역전파 계산 시에도 Convolution 연산이 나온다.
- 각 커널에 들어오는 모든 그레디언트를 더하면 결국 Convolution 연산과 같다.
- 피어세션 회의 내용
#NN과 MLP의 차이
- NN은 신경망으로 대부분 하나의 은닉층을 가진 평범한 신경망을 의미한다.
- 두 개 이상의 Hidden Layer로 구성되어 있으면 MLP라고 한다.
# M.train
- 모델 내의 파라미터들이 required_grad가 true로 변경해 train mode로 변경한다.
- eval 시에는 false로 변경해서 test mode로 변경한다.
# backward를 갱신한 값을 옵티마이저 객체에 넣지 않고 어떻게 사용하는가?
- backward()는 tensor 객체로, tensor 안에 자동으로 누적이 되어 굳이 따로 연동을 하지 않아도 상관없다.
- 해야할 일
왜 파라미터 수의 범위가 좁으면 더 좋은 학습 효율이 보이는가?
- 데이터의 수치가 넓다면, 데이터의 크기가 들쑥날쑥해지는데 모델이 데이터를 이상하게 해석할 우려가 있다.
- 또한 수치가 높은 데이터를 모델이 중요하게 생각해서 이상한 해석이 나올 수 있다.
- 이를 위해 데이터를 같은 정도의 중요도를 반영하도록 정규화해야 한다.
'BOOSTCAMP AI TECH > 3주차_Deep Learning Basics' 카테고리의 다른 글
| [BOOSTCAMP AI TECH] 15일차_Generative model (0) | 2021.02.07 |
|---|---|
| [BOOSTCAMP AI TECH] 14일차_Recurrent Neural Network (0) | 2021.02.04 |
| [BOOSTCAMP AI TECH]13일차_Convolution Neural Network (0) | 2021.02.03 |
| [BOOSTCAMP AI TECH] 11일차_딥러닝 기초 (0) | 2021.02.01 |



