book.naver.com/bookdb/book_detail.nhn?bid=16238302
파이썬 머신러닝 완벽 가이드
자세한 이론 설명과 파이썬 실습을 통해 머신러닝을 완벽하게 배울 수 있습니다!《파이썬 머신러닝 완벽 가이드》는 이론 위주의 머신러닝 책에서 탈피해 다양한 실전 예제를 직접 구현해 보면
book.naver.com
*해당 글은 학습을 목적으로 위의 도서 내용 중 일부 내용만을 요약하여 작성한 포스팅입니다.
상세한 내용 및 전체 내용 확인을 원하신다면 도서 구매를 추천드립니다.
군집화
- 데이터에 대한 레이블이 지정되어 있지 않을 때, 데이터를 그룹핑하는 분석 알고리즘
- 데이터들의 특성을 고려해 데이터 집단(클러스터)를 정의하고, 데이터 집단을 대표하는 중심점을 찾는 데이터 마이닝
*클러스터 : 비슷한 특성을 가진 데이터의 집합
*특성이 다른 데이터들은 서로 다른 클러스터에 속한다.
*분류는 라벨이 있는 데이터를 활용한 지도 학습이고, 군집화는 라벨이 없는 데이터를 활용한 비지도 학습이다.
K-평균 군집화 (K-means Clustering)
- 가장 일반적으로 사용되는 알고리즘
- 거리 기반 군집화이다.
K-평균 군집화 작동 방식
- 군집 중심점 (centroid)라는 특정한 임의의 지점을 선택해 해당 중심에 가장 가까운 포인트들을 선택한다.
- 선택된 포인트의 평균 지점으로 군집 중심점을 이동하고, 이동된 중심점에서 다시 가까운 포인트를 선택해 다시 중심점을 평균 지점으로 이동
- 위의 두 프로세스를 반복 실행
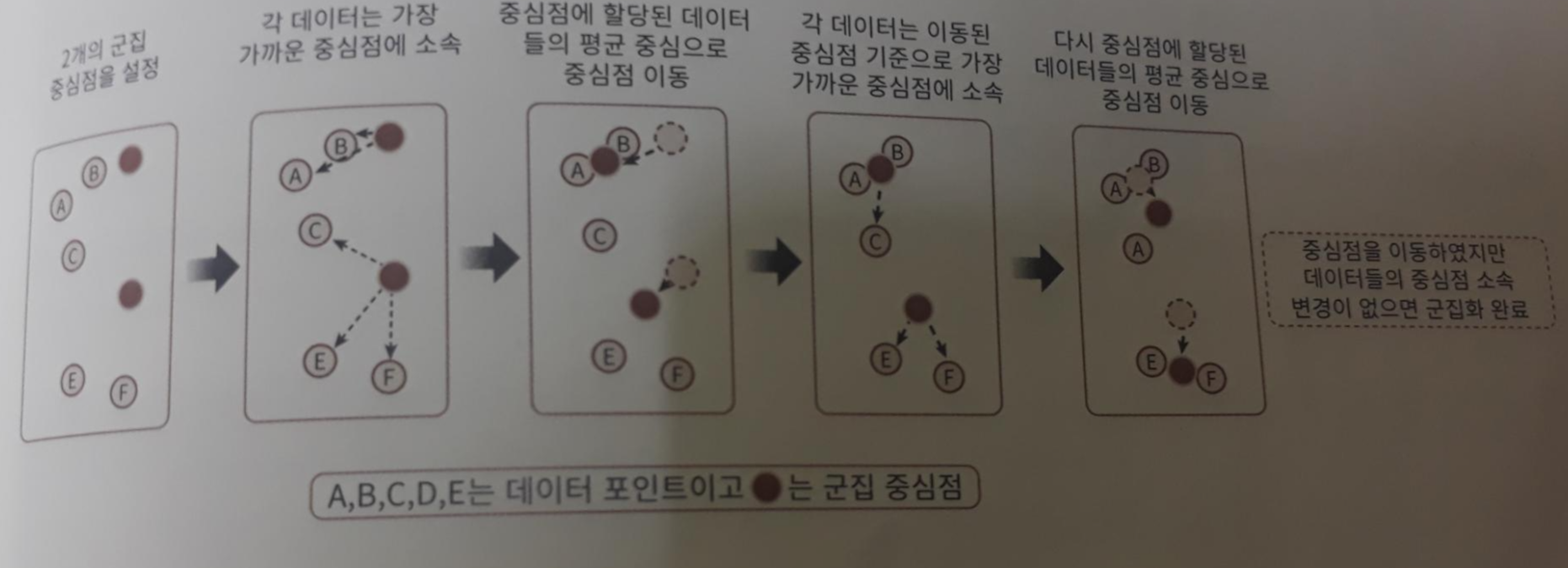
- 군집화의 기준이 되는 중심점을 구성하려는 군집화 개수 n개만큼 임의의 위치에 놓는다.
- 각 데이터는 각 위치에서 가장 가까운 중심점에 소속된다.
- 소속이 결정되면 군집 중심점을 소속된 평균 중심으로 이동한다.
- 각 데이터는 다시 자신의 위치에서 가장 가까운 중심점에 소속된다.
- 다시 군집 중심점을 소속된 평균 중심으로 이동한다.
- 중심점을 이동했는데 데이터의 중심점 소속 변경이 없다면 군집화를 종료한다. 아닐경우 반복한다.
*처음 임의의 위치에 군집 중심점을 놓으면 반복적인 이동 횟수가 너무 많아 초기화 알고리즘으로 적합한 위치에 중심을 가져다 놓는 방법이 필요하다.
*가장 대표적인 방법은 K-means++인데, 데이터 중 임의의 한 데이터를 중심점으로 삼고, 해당 점에서 가장 먼 점을 다음 중심점으로 잡아가는 과정을 k번 반복한 방법.
*sklearn.cluster.KMean의 경우에는 init 파라미터로 설정이 가능한다. 그런데 디폴트 값이 k-means++라 건들 건 없음. (k-means++ | random)
*K-Means는 처음 군집 중심점의 갯수를 정하는 것도 중요한데, 그 방법에는 Elbow Method, 손실함수, 실루엣 계수 등을 이용한다.
steadiness-193.tistory.com/285
K-평균의 장점과 단점
- 장점
- 일반적인 군집화에서 가장 많이 활용되는 알고리즘이다.
- 쉽고 간결하다.
- 데이터가 원형으로 흩어져 있는 경우 효과적이다.
- 단점
- 거리 기반 알고리즘으로 속성의 수가 많으면 군집화 정확도가 떨어진다.
- 반복으로 수행해서 반복 횟수가 많을 수록 수행 시간이 느려짐.
- 초기에 선택해야 할 군집의 개수를 선정하기 어려움.
- 길죽한 데이터에 대해서는 효과적이지 못하다.
- 이상값에 민감하다.
*속성의 수가 너무 많으면 PCA로 차원 감소를 적용해야 할 수도 있다.
사이킷런의 K-Means
- sklearn.cluster.KMeans(n_clusters=8, *, init='k-means++', n_init=10, max_iter=300, tol=0.0001, precompute_distances='deprecated', verbose=0, random_state=None, copy_x=True, n_jobs='deprecated', algorithm='auto')
*n_clusters : 군집화할 개수
*init : 초기 군집 중심점의 좌표 설정 방식 (보통 임의로 중심을 설정하지 않고 디폴트값 사용)
*max_iter : 최대 반복 횟수
평균 이동 (Mean Shift)
- K 평균과 유사하게 중심을 군집의 중심으로 지속적으로 움직이며 군집화 수행
- K 평균이 중심에 소속된 데이터의 평균 거리 중심으로 이동하는 데 반해, 평균 이동은 중심을 데이터가 모여 있는 밀도가 가장 높은 곳으로 이동한다.
- 즉, 데이터의 분포도를 이용해 군집 중심점 탐색. (데이터 포인트가 모여있는 곳)
- 이를 위해 확률 밀도 함수를 이용하는데, 확률 밀도 함수가 가장 높은 곳을 중심점으로 선정한다.
- 일반적으로 주어진 모델의 확률 밀도 함수를 찾기 위해 KDE를 사용.
평균 이동 작동 방식
- 특정 데이터를 반경 내의 데이터 분포 확률 밀도가 가장 높은 곳으로 이동하기 위해 주변 데이터와의 거리 값을 KDE 함수 값으로 입력한 뒤, 그 반환 값을 현재 위치에서 업데이트하면서 이동한다.
- 이러한 방식을 전체 데이터에 반복적으로 적용해 군집 중심점 탐색한다.

- 초기 군집 중심점과 대역폭 설정
- 대역폭 내의 데이터 분포도를 KDE 기반의 평균 이동 알고리즘으로 계산
- 계산된 데이터 분포도가 높은 방향, 즉 데이터 밀도가 높은 곳으로 중심점 이동.
- 위의 과정을 반복하며 가장 데이터 밀도가 높은 지점을 기준으로 군집화 수행.
작동 방식 확인
www.kdnuggets.com/2018/06/5-clustering-algorithms-data-scientists-need-know.html
KDE (Kernel Density Estimation)
- 커널 함수를 통해 어떤 변수의 확률 밀도 함수를 추정하는 방법
- 관측된 데이터 각각에 커널 함수를 적용한 값을 모두 더한 뒤 데이터 건수로 나눠 확률 밀도 함수를 추정한다.
- 커널 함수는 대표적으로 가우시안 분포 함수가 사용된다.
*확률 밀도 함수 (PDF)
-확률 변수의 분포
-확률 밀도 함수를 통해 특정 변수가 어떤 값을 갖게 될지에 대한 확률을 알 수 있다.
-감마 분포, T-분포 등
KDE의 식
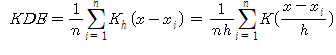
- K : 커널 함수 / x : 확률 변숫값 / xi : 관측값 / h : 대역폭
- 적절한 대역폭 h를 계산하는 것이 중요하다.
- h가 작으면 군집 중심점이 많이 생겨 작고 뾰족한 KDE가 생긴다.
- h가 작으면 변동성이 커져 과적합하기 쉽다.
- h가 크면 군집 중심점이 너무 적어 평활화된 KDE가 생긴다.
- h가 크면 지나치게 단순화되어 과소적합하기 쉽다.
- 평균 이동 군집화는 군집의 개수를 사전에 지정하지 않으며, 오로지 대역폭의 크기에 따라 군집화를 수행한다.

평균 이동의 장점과 단점
- 장점
- 분석에 앞서 데이터 세트에 대한 가정을 하지 않기에 유연한 군집화가 가능하다.
- 이상치의 영향력이 크지 않고, 미리 군집의 개수를 정할 필요가 없다.
- 단점
- 알고리즘의 수행 시간이 오래 걸린다.
- 대역폭의 크기에 따른 군집화 영향도가 매우 크다.
사이킷런의 평균 이동
- sklearn.cluster.MeanShift(*, bandwidth=None, seeds=None, bin_seeding=False, min_bin_freq=1, cluster_all=True, n_jobs=None, max_iter=300)
- bandwidth가 대역폭 h이다.
*최적의 대역폭 계산을 위해 sklearn.cluster.estimate_bandwidth 함수가 있다.
*estimate_bandwidth(X, *, quantile=0.3, n_samples=None, random_state=0, n_jobs=None)
GMM (GAUSSIAN Mixture Model)

- 군집화를 적용하고자 하는 데이터가 여러 개의 가우시안 분포를 가진 데이터 집합이라 가정
- 데이터 분포에서 개별 유형의 가우시안 분포를 추출한다.
- 전체 데이터 세트에서 여러 가우시안 분포를 구한 후 각 데이터가 어떤 가우시안 분포에 속할지 확률 추정
*가우시안 분포 (정규 분포) : 과우 대칭형의 종 형태의 연속 확률 함수
*평균을 중심으로 높은 분포도를 가지고 있다.
GMM의 동작 방식
- 전체 데이터에 대해 여러 개의 정규 분포 곡선을 추출한다.
- 개별 데이터가 어떤 정규 분포에 속하는지 결정한다.
- 위의 과정을 모수 추정이라 한다.
*모수 추정 : 관측된 데이터로 모집단을 추리하는 것 (일부로 전체를 추리)
*모수 추정은 대표적으로 개별 정규 분포의 평균과 분산, 각 데이터가 어떤 정규 분포에 속하는지에 대한 확률을 추정한다.
*모수 추정이 어떤 정규 분포에 속하는지에 대한 확률을 추정하기에 GMM은 확률 기반 군집화이다.
- GMM은 모수 추정을 위해 EM 방식을 사용한다.
*EM (기댓값 최대화 알고리즘) : 관측되지 않는 잠재변수에 의존하는 최대가능도나 최대사후확률을 갖는 모수의 추정값을 찾는 알고리즘
GMM의 장점과 단점
- 장점
- K 평균보다 유연하게 다양한 데이터 세트에 잘 적용될 수 있다.
- 예를 들면 길쭉한 데이터 분포에도 잘 적용된다.
- 단점
- K 평균과 달리 군집의 중심 좌표를 구할 수 없어 군집 중심 표현의 시각화가 불가능하다.
- 시간이 오래 걸린다.
사이킷런의 GMM
- sklearn.mixture.GaussianMixture(n_components=1, *, covariance_type='full', tol=0.001, reg_covar=1e-06, max_iter=100, n_init=1, init_params='kmeans', weights_init=None, means_init=None, precisions_init=None, random_state=None, warm_start=False, verbose=0, verbose_interval=10)
- 가장 중요한 파라미터는 n_components인데, 이는 모델의 총 개수로 군집의 개수를 정하는 데 중요한 역할을 한다.
DBSCAN (Density Based Spatial Clustering of Applications with Noise)
- 간단하고 직관적인 알고리즘이나, 복잡한 기하학적 분포도를 가진 데이터 셋에 대해서도 효과적인 군집화가 가능
DBSCAN의 동작 방식
- 입실론 주변 영역의 최소 데이터 개수를 포함하는 밀도 기준을 충족시키는 데이터인 핵심 포인트를 연결해가며 군집화를 구성한다.
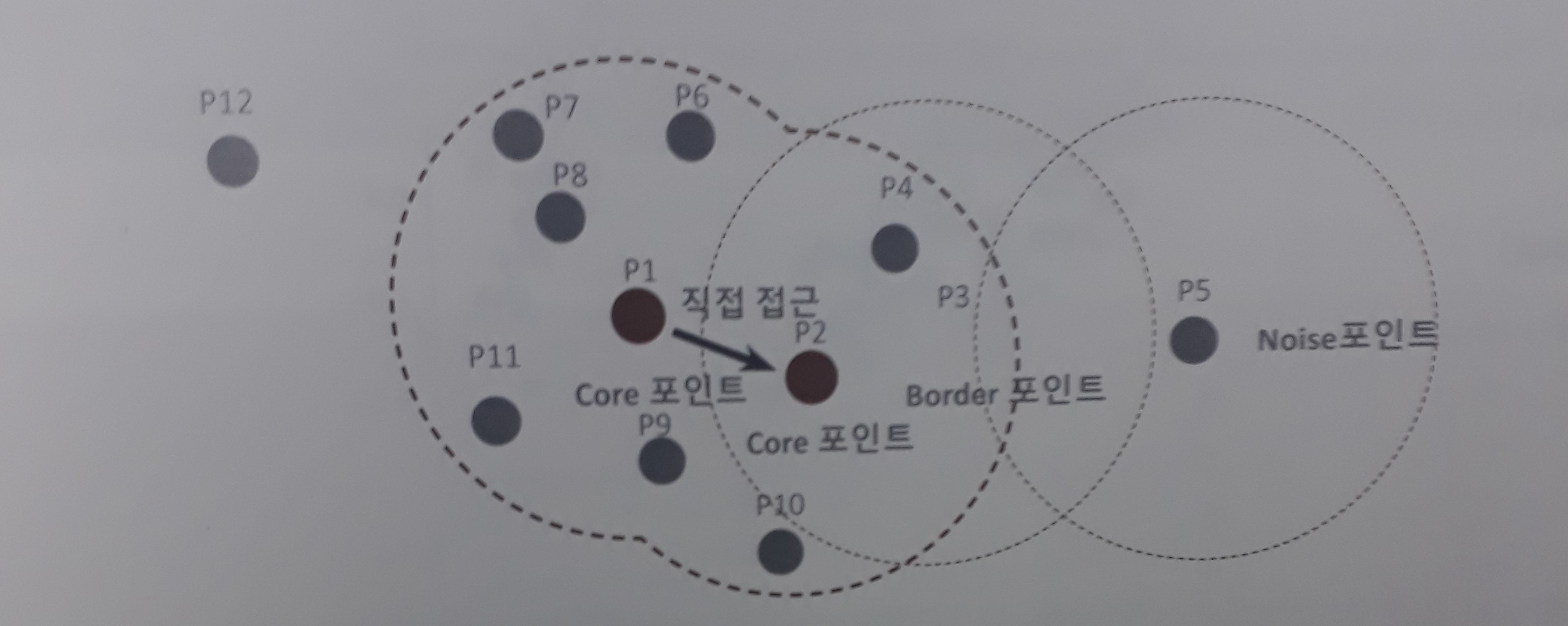
- 입실론 영역의 넓이와 최소 데이터 개수 선정한다.
- 순서대로 각 데이터를 기준으로 입실론 영역 내 데이터의 개수가 최소 데이터 개수 이상인지 확인하고 아래의 분기를 따른다.
- 만약 만족하면 해당 데이터는 핵심 포인트.
- 만약 입실론 영역 안에 이웃 포인트로 핵심 포인트 존재 시 두 핵심 포인트를 연결해 군집을 통합.
- 만약 핵심 포인트 조건에 만족하지 못한 데이터 존재할 경우 아래의 분기 실행.
- 해당 데이터의 입실론 영역 인근에 핵심 포인트 존재시 경계 포인트
- 핵심 포인트 미존재시 잡음 포인트로 취급
*입실론 주변 영역 : 개별 데이터를 중심으로 입실론 반경을 가지는 원형의 영역
*최소 데이터 개수 : 개별 데이터의 입실론 주변 영역에 포함되어야 하는 타 데이터 개수 (본인 포함)
*핵심 포인트 : 주변 영역 내에 최소 데이터 개수 이상의 타 데이터를 가진 포인트
*이웃 포인트 : 주변 영역 내에 위치한 타 데이터
*경계 포인트 : 핵심 포인트가 아니지만 핵심 포인트를 이웃 포인트로 가진 데이터
*잡음 데이트 : 핵심 포인트가 아니며, 이웃 포인트 중 핵심 포인트가 아닌 데이터
DBSCAN의 장점과 단점
- 장점
- K Means와 같이 클러스터의 수를 정하지 않아도 된다.
- 클러스의 밀도에 따라 클러스터를 연결해 기하학적인 모양을 갖는 군집도 잘 찾는다.
- 단점
- 속도가 느리다.
- eps와 min_samples의 영향을 많이 받는다.
- 유클리드 제곱 거리를 사용하는데, 이로 인해 Curse Of dimensionality 또한 존재한다.
*Curse Of Dimensionality (차원의 저주)
차원이 늘어남에 따라 계산량과 메모리 사용량이 빠르게 증가하여 계산 불가 상태에 빠지는 현상.
차원이 늘어남에 따라 데이터의 거리가 멀어져 밀집도가 작아지는 현상
이 외에도 차원이 늘어남에 따라 나타나는 다양한 문제점들을 통틀어 차원의 저주라 부른다.
저차원의 데이터는 문제가 되지 않지만, 고차원의 데이터에서는 문제가 된다.
*PCA, LDA, LLE 등 차원축소를 통해 해결할 수 있다.
사이킷런의 DBSCAN
- sklearn.cluster.DBSCAN(eps=0.5, *, min_samples=5, metric='euclidean', metric_params=None, algorithm='auto', leaf_size=30, p=None, n_jobs=None)
*eps : 입실론 주변 영역의 반경
*min_samples : 핵심 포인트가 되기 위한 최소 이웃 포인트 수 (min points + 1)
*eps가 줄어들수록 노이즈 데이터 수가 많아진다.
*min_samples 수가 늘어날수록 노이즈 데이터가 많아진다.
군집화 알고리즘 테스트를 위한 데이터 생성
- 사이킷런은 다양한 유형의 군집화 알고리즘 테스트를 위한 간단한 데이터 생성기를 제공한다.
- sklearn.datasets 모듈 안에 속해있다.
함수들
make_blobs

- 등방성 가우시안 정규 분포를 이용해 가상 데이터 생성
- sklearn.datasets.make_blobs(n_samples=100, n_features=2, *, centers=None, cluster_std=1.0, center_box=- 10.0, 10.0, shuffle=True, random_state=None, return_centers=False)
*n_samples : 생성할 총 데이터 개수
*n_features : 데이터 특성 개수. 일반적으로 2개를 설정해 첫 번째는 x좌표, 두 번째는 y좌표로 사용
*centers : int 값으로 설정시 군집의 개수 / ndarray로 표현시 개별 군집 중심점
*cluster_std : 생성될 군집 데이터의 표준 편차
*return 값은 튜플
*등방성 : 모든 방향으로 같은 성질을 가진다.
make_moons

- 초승달 모양의 데이터 클러스터 두 개 생성
- sklearn.datasets.make_moons(n_samples=100, *, shuffle=True, noise=None, random_state=None)
*n_samples : 생성할 총 데이터 개수
*noise : 잡음의 크기. 0이면 정확히 반원
make_circles
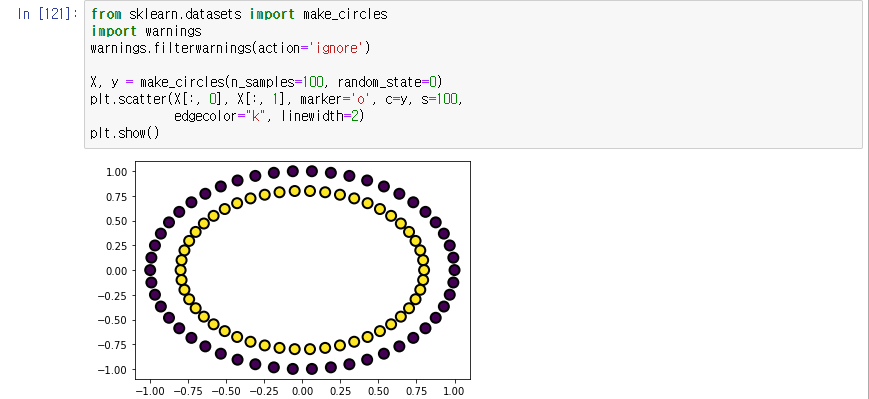
- 작은 원과 큰 원으로 이루어진 데이터 생성
- sklearn.datasets.make_circles(n_samples=100, *, shuffle=True, noise=None, random_state=None, factor=0.8)
*n_samples : 생성할 총 데이터 개수
*noise : 노이즈 데이터 세트의 비율
*factor : 외부 원과 내부 원의 scale 비율
make_gaussian_quantiles

- 다차원 가우시안 분포의 표본을 생성하고 분포의 기대값을 중심으로 한 등고선의 클래스로 분리
- sklearn.datasets.make_gaussian_quantiles(*, mean=None, cov=1.0, n_samples=100, n_features=2, n_classes=3, shuffle=True, random_state=None)
*mean : 기댓값 벡터
*cov : 공분산 행렬
*n_samples : 생성할 총 데이터 개수
*n_features : 독립 변수의 수
*n_classes : 클래스의 수
*return 값은 [n_samples, n_features]의 독립 변수, [n_samples]의 종속 변수
make_classification

- 분류용 가상 데이터 생성
- sklearn.datasets.make_classification(n_samples=100, n_features=20, *, n_informative=2, n_redundant=2, n_repeated=0, n_classes=2, n_clusters_per_class=2, weights=None, flip_y=0.01, class_sep=1.0, hypercube=True, shift=0.0, scale=1.0, shuffle=True, random_state=None)
*n_samples : 생성할 총 데이터 개수
*n_features : 독립 변수의 수
*n_informative : 독립 변수 중 종속 변수와 상관 관계가 있는 성분의 수
*n_redundant : 독립 변수 중 다른 독립 변수의 선형 조합으로 나타나는 성분의 수
*n_repeated : 독립 변수 중 단순 중복된 성분의 수
*n_classes : 종속 변수의 클래스 수
*n_clusters_per_class : 클래스 당 클러스터의 수
*weights : 각 클래스에 할당된 표본 수
*random_state : 난수 발생 시드
*return 값은 [n_samples, n_features]의 독립 변수, [n_samples]의 종속 변수
군집 평가
- 군집화는 분류와 유사해보일 수 있으나 성격이 다르다.
- 군집화는 동일한 분류 값에 속하더라도 더 세분화한 군집화를 추구할 수 있고, 서로 다른 분류의 값도 넓은 군집으로 합칠 수 있기 때문.
- 그래서 군집화의 효율성을 평가하기 위해서는 분류의 것과 다른 별도의 지표가 필요하다.
실루엣 분석
- 군집화 평가 방법의 대표적인 방법
- K 평균 군집화에서 군집의 갯수를 정하기 위해 사용한다.
- 군집화한 결과의 군집 간 거리가 얼마나 효율적으로 분리되어 있는지를 나타낸다.
- 효율적으로 잘 분리가 되었다는 것은 다른 군집과는 멀리 떨어져있고, 동일 군집 간 데이터는 잘 뭉쳐 있음을 의미한다.
- 즉, 군집화가 잘 되었으면 개별 군집들이 비슷한 여유공간을 가지고 떨어진다.
- K 평균은 개별 군집별로 적당히 분리된 거리를 유지하며 군집 내 데이터가 서로 뭉쳐 있어야 적절한 군집 개수가 설정되었다 판단할 수 있다.
실루엣 분석 식
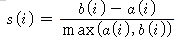
- a(i) : 동일 군집 내 다른 데이터들과의 거리의 평균
- b(i) : 타 군집 중 가장 가까운 군집과의 평균 거리
- b(i) - a(i)는 두 군집 간의 떨어진 거리이다.
- max로 나누는 것은 떨어진 거리를 정규화 하기 위함이다.
실루엣 계수의 값

- 실루엣 계수는 -1~1의 범위를 가지며, 1에 가까울수록 근처의 군집과 멀리 떨어져 있고, 0에 가까울수록 근처의 군집과 가까움을 뜻한다.
- 만약 음수는 아예 다른 군집에 데이터 포인트가 할당되어 있음을 의미한다.
- 즉 1에 가까울수록 좋은 것인데, 그렇다고 평균 실루엣 계수 값이 높다고 반드시 최적의 군집 개수로 군집화가 된 것은 아니다.
- 특정 군집 내의 실루엣 계수 값만 너무 높고, 다른 군집은 내부 데이터끼리의 거리가 떨어져 있으면 실루엣 계수 값이 낮아져도 평균적으로 높은 값이 나올 수 있기 때문.
실루엣 계수의 장점과 단점
- 장점 : 직관적으로 이해하기 쉽다.
- 단점 : 각 데이터 별로 다른 데이터와의 거리를 반복해서 계산하기에 수행 시간이 길고 메모리 사용이 많다.
*데이터가 많을수록 성능이 떨어지는데, 이럴 때는 군집별로 임의의 데이터를 샘플링해 실루엣 계수를 평가해야 한다.
사이킷런에서의 실루엣 분석
- sklearn.metrics.silhoutte_samples(X, label, metric='euclidean', **kwds)
- x 피처 데이터 셋과 각 피처 데이터 셋이 속한 군집 레이블 값인 label을 주면 각 데이터 포인트의 실루엣 계수를 반환한다.
- sklearn.metrics.silhouette_score(X, labels, metric='euclidean', sample_size=None, **kwds)
- x 피처 데이터 셋과 label 데이터 입력시 전체 데이터의 실루엣 계수 값을 평균해 반환한다.
- 즉, np.mean(silhouette_samples())과 같다.
- 앞서 언급했듯 무조건 값이 높다고 군집화가 잘 된것은 아니다.

