book.naver.com/bookdb/book_detail.nhn?bid=16238302
파이썬 머신러닝 완벽 가이드
자세한 이론 설명과 파이썬 실습을 통해 머신러닝을 완벽하게 배울 수 있습니다!《파이썬 머신러닝 완벽 가이드》는 이론 위주의 머신러닝 책에서 탈피해 다양한 실전 예제를 직접 구현해 보면
book.naver.com
*해당 글은 학습을 목적으로 위의 도서 내용 중 일부 내용만을 요약하여 작성한 포스팅입니다.
상세한 내용 및 전체 내용 확인을 원하신다면 도서 구매를 추천드립니다.
회귀
- 회귀 분석은 데이터 값이 평균과 같은 일정한 값으로 돌아가려는 경향을 이용한 통계학 기법이다.
- 여러 개의 독립변수에 따라 종속변수가 어떤 관계를 나타내는지 모델링하고 예측한다.
- Y = W(1)*X(1) + W(2)*X(2) + ... + W(n)*X(n)에서 Y는 종속변수, X는 독립변수, W는 독립변수에 영향을 미치는 회계 계수이다.
독립변수는 피처에 해당되며 종속변수는 결정 값이다.
회귀 예측의 특징은 최적의 회귀 계수를 찾아내는 것이다.
회귀의 종류
- 독립변수의 개수에 따라 단일 회귀(독립변수 한 개), 다중 회귀로 나뉜다.
- 회귀계수의 결합에 따라 선형 회귀와 비선형 회귀로 나뉜다.
- 일반적으로 선형 회귀가 가장 많이 사용된다.
- 선형 회귀는 규제 방법에 따라 다시 별도의 유형으로 나뉜다.
*선형 회귀 : 실제 값과 예측 값의 차이 (오류의 제곱)를 최소화 하는 직선형 회귀선을 최적화하는 방식
*규제 : 일반적인 선형 회귀의 과적합 문제를 해결하기 위해 회귀 계수에 패널티 적용
일반 선형 회귀
- 예측값과 실제 값의 RSS (Residual Sum of Squares)를 최소화할 수 있도록 회귀 계수를 최적화하며, 규제를 하지 않은 모델
릿지 (Rdige)
- 선형 회귀에 L2 규제를 결합한 회귀 모델
- L2 모델은 상대적으로 큰 회귀 계수 값의 예측 영향도를 감소시키기 위해 회귀 계수값을 더 작게 만드는 규제 모델
라쏘 (Lasso)
- 선형 회귀에 L1 규제를 결합한 모델
- L2 규제가 회귀 계수 값의 크기를 줄이는 데 반해, L1 규제는 예측 영향력이 작은 피처의 회귀 계수를 0으로 만들어 피처가 선택되지 않게 한다.
- L1 규체는 피처 선택 기능으로도 불린다.
엘라스틱넷 (ElastricNet)
- L1, L2 규제를 함께 결합한 모델
- 주로 피처가 많은 데이터 세트에 적용되며, L1 규제로 피처의 개수를 줄이고 L2 규제로 계수 값의 크기를 조정
로지스틱 회귀 (Logistic Regression)
- 매우 강력한 분류 알고리즘
- 일반적인 이진 분류 뿐 아니라 희소 영역 분류에도 뛰어난 예측 성능을 보임
단순 선형 회귀를 통한 회귀 이해
- 단순 선형 회귀란 독립 변수도 하나, 종속 변수도 하나인 선형 회귀
- 데이터를 직선 형태 (선형)의 그래프로 관계를 표현할 수 있다.
- 실제 값과 회귀 모델의 차이(잔차, 오류 값)를 최소화하는 회귀 계수를 찾는다.
- 오류 값(잔차)를 계산할 때는 절대값을 취해서 더하거나 (Mean Absolute Error), 혹은 제곱을 구해서 더하는 형식이 있다. (RSS, Residual Sum of Square)
- 일반적으로 미분 등의 계산을 편하게 하기 위해 RSS 방식을 사용한다.
- (error)^2 = RSS
- 회귀에서 RSS는 비용(cost)라고 불리고, w 변수(회귀 계수)로 구성되는 RSS를 비용 함수라고 한다.
- 회귀의 목적은 데이터를 계속 학습하며 이 비용함수가 반환하는 오류 값을 줄여 최소의 오류 값을 구하는 것
- 이 때 비용 함수는 손실 함수라고도 한다.
경사 하강법
- 비용 함수가 최소가 되는 W 파라미터(회귀 계수)를 구하는 과정
- 회귀 계수의 수가 적다면 고차원 방정식으로 도출이 가능하지만, 많으면 해결이 어렵다.
- 경사 하강법은 고차원 방정식에 대한 문제를 해결해주며 RSS를 최소화 하는 방법을 직관적으로 제공한다.
- 점진적이고 반복적인 계산으로 회귀 계수 값을 업데이트하며 보정한다.
- 그리고 오류 값을 계속해서 적게 만들고, 오류 값이 더 이상 작아지지 않으면 해당 오류 값을 최소 비용으로 판단하고 최적 파라미터로 반환한다.
경사 하강법 과정

LinearRegression
- 예측값과 실제 값의 RSS를 최소화해 OLS 추정 방식으로 구현한 클래스.
- sklearn.linear_model.LinearRegression(fit_intercept=True, normalize=False, copy_X=True, n_jobs=1)
*fit_intercept : intercept(절편) 값을 계산할지 말지 지정
*normalize : fit_intercept가 false이면 무시. 회귀를 수행하기 전 입력 데이터를 정규화할지 결정
*output은 coef_ : 회귀 계수가 (target 값 개수, 피처 개수)의 배열 형태로 반환
*intercept_ : 절편값
회귀 평가 지표
- 회귀 평가의 지표는 실제 값과 회귀 예측값의 차이 값을 기반으로 한 지표가 중심.

*MSE나 RMSE에 로그를 적용한 MSLE, RMSLE도 사용한다.
*사이킷런은 RMSE를 제공하지 않는다. 그래서 RMSE 사용을 위해서는 MSE에 제곱근을 씌워 사용해야 한다.
다항 회귀
- 2차, 3차 방정식과 같이 다항식으로 표현되는 회귀
- 사이킷런은 다항 회귀를 위한 클래스를 명시적으로 제공하지 않는다.
- 다만 다항 회귀 역시 선형 회귀이기 때문에 비선형 함수를 선형 모델에 적용시키는 방법으로 구현할 수 있다.
- 이를 위해 사이킷런은 PolynomialFeatures 클래스를 통해 피처를 Polynomial(다항식) 피처로 변환한다.
*다항 회귀는 선형 회귀이다.
*선형/비선형 회귀를 나누는 기준은 회귀 계수의 선형 여부이지, 독립변수의 선형 여부가 아니기 때문.
*PolynomialFeatures(degree=3)은 [x1, x2]를
3차 다항 계수 [1, x1, x2, x1^2, x1x2, x2^2, x1^3, x1^2x2, x1x2^2, x2^3]과 같이 표현
*model = Pipeline([('poly', PolynomialFeatures(degree=3)), ('linear', LinearRegression())])
과소적합과 과적합
- 과소적합 : 학습 데이터의 패턴을 지나치게 단순화
- 과대적합 : 학습 데이터의 패턴을 하나하나 감안한 지나치게 복잡한 모델
- 과대적합은 차수가 높아질수록 발생한다.
편향-분산 트레이드오프(Bias-Variance Trade-off)
- 편향이 낮으면 예측 결과가 실제 결과와 근접하다.
- 편향이 높으면 예측 결과가 실제 결과에서 벗어난다.
- 분산이 낮으면 예측 결과가 특정 부분에 집중된다.
- 분산이 높으면 예측 결과가 넓은 부분에 분포된다.
- 편향이 높으면 분산이 낮아져 과소적합이 일어난다.
- 분산이 높으면 편향이 낮아져 과대적합이 일어난다.
- 편향과 분산이 서로 트레이드오프를 이루며 오류 cost 값이 최소점인 모델을 구축해야 한다.
규제 선형 모델
- 앞선 선형 모델은 RSS를 최소화 하는 부분만 고려한다.
- 이럴 경우 학습 데이터에 지나치게 맞고 회귀 계수가 커져서 변동성이 심해져 과적합이 일어난다.
- 이에 비용 함수를 통해 RSS를 최소화하며 과적합을 방지해야 한다.
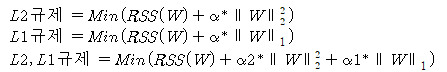
- alpha 값을 크게 하면 비용 함수는 회귀 계수 w의 값을 작게 해 과적합 개선
- alpha 값을 작게 하면 회귀 계수 w의 값이 커져도 상쇄가 가능해 학습 데이터 적합 개선
- 규제란 alpha 값으로 패널티를 부과해 회귀 계수 값의 크기를 감소시켜 과적합을 개선하는 방식이다.
- L2 규제는 W의 제곱에 대해 패널티를 부여하는 방식이다.
- L1 규제는 W의 절댓값에 패널티를 부여하는 방식이다.
릿지 회귀
- L2 규제를 적용한 회귀
- sklearn.linear_model.Ridge 클래스를 사용한다.
- 주요 파라미터는 alpha이며, L2 규제 계수에 해당한다.
- alpha의 크기가 클수록 회귀 계수가 작아진다.
라쏘 회귀
- L1 규제를 적용한 선형 회귀
- L2 규제는 회귀 계수의 크기를 감소시키는데 반해, L1 규제는 불필요한 회귀 계수를 감소시켜 0으로 만들고 제거한다.
- L1 규제는 적절한 특징만 회귀에 포함시키는 피처 선택의 특성을 갖고 있다.
- sklearn.linear_model.Lasso 클래스를 사용한다.
- 파라미터 alpha는 L1 규제 계수이다.
- alpha의 크기가 클수록 0으로 만드는 특징들이 많아진다.
엘라스틱넷 회귀
- L2 규제와 L1 규제를 함께 결합한 회귀
- 라쏘 회귀가 중요 피처만을 선택하는 과정에서 회귀 계수의 값이 급격하게 변동하는 현상을 완화하기 위해 L2 규제를 추가
- 수행시간이 상대적으로 오래걸린다.
- sklearn.linear_model.ElasticNet 클래스를 사용한다.
- 파라미터는 alpha와 l1_ratio이다.
- 엘라스틱넷의 규제는 a*l1 + b*l2 인데, a는 l1의 규제값, b는 l2의 규제값이다.
- l1_ratio는 a / (a+b)인데, 0이면 a가 0이므로 L2 규제와 동일하고, 1이면 b가 0이라 L1 규제와 동일하다.
로지스틱 회귀

- 선형 회귀 방식을 분류에 적용한 알고리즘
- 선형 회귀 방식을 기반으로 시그모이드 함수를 이용해 분류를 수행하는 회귀
- 가볍고 빠르며, 이진 분류 예측 성능 뿐 아니라 희소한 데이터 세트 분류에도 뛰어난 성능을 보인다.
- sklearn.linear_model.LogisticRegression 클래스를 사용한다.
- 주요 파라미터는 penalty, C이다.
- penalty는 규제 유형이며, 기본으로는 l2이고, l2이면 L2규제, l1이면 L1규제
- C는 규제 강도로, C값이 작을수록 규제 강도가 커진다.
회귀 트리
- 선형 회귀는 회귀 계수를 선형으로 결합하는 회귀 함수를 구해 독립변수를 입력해 결과값을 예측한다.
- 비선형 회귀는 비선형 회귀 함수를 통해 결과값을 예측한다.
- 비선형 회귀는 회귀 계수의 결합이 비선형이다.
- 트리 기반의 회귀는 회귀를 위한 트리를 생성하고 이를 기반으로 회귀 예측을 한다.
- 분류 회귀와 다른 점은 리프 노드에서 클래스 레이블을 결정하지 않고, 리프 노드에 속한 데이터 값의 평균값을 구해 회귀 예측값을 계산하는 점.
- 선형 회귀는 직선으로 예측 회귀선을 표현하는데, 회귀 트리는 분할되는 데이터 지점에 따라 브랜치를 만들며 계단 형태로 회귀선을 만든다.
*트리 생성이 CART 알고리즘에 기반되어 있어 결정트리, 랜덤 포레스트, GBM도 분류 뿐 아니라 회귀가 가능하다.
*DecisionTreeRegressor / DecisionTreeClassifier
실습코드 : https://github.com/123okk2/MachineLearning_practice/tree/main/5.%20%ED%9A%8C%EA%B7%80


