- 강의 목록
-시각화 도구
-통계학 맛보기
- 요약
강의
matplot.pyplot과 serborn 라이브러리를 사용하여 데이터를 시각화 하는 방법을 학습했다.
모수, 확률분포, 가능도 등 확률 관련 수학을 학습했다.
피어세션
어제 배운 내용을 정리하며 다시 한 번 학습하는 시간을 가졌다.
- 학습정리
Matplot
- Pyplot이라는 객체를 사용해 데이터 표시한다.
- 구체적으로는 Pyplot 객체에 그래프를 쌓은 다음 flush하는 방식이다. 이 때 그래프는 화면에 보여준 후 메모리에 남겨두지 않는다.
- 단점으로는 argument를 kwargs로 받는데, 고정된 argument가 없어 alt+tab으로 확인이 어렵다.
- 그래프는 원래 figure 객체에 생성
import matplotlib.pyplot as plt
import numpy as np
x = range(100)
y = x
plt.plot(x, y)
plt.show()
y_1 = [np.cos(value) for value in x]
y_2 = [np.sin(value) for value in x]
plt.plot(x, y_1)
plt.plot(x, y_2)
#plt.plot(range(100), range(100))
plt.show()
Figure & Axes
- pyplot 객체 사용시 기본 figure에 그래프가 그려진다.
- Matplotlib은 figure안에 axes로 구성하고, figure 위에 여러 개의 axes를 생성한다.
- 즉, 그냥하면 한 표 안에 여러 그래프가 출력되지만 figure 사용시 여러 표에 각각 하나의 그래프가 출력된다.
fig = plt.figure()
fig.set_size_inches(5,2) #크기 지정
ax_1 = fig.add_subplot(1,2,1) #두 개의 plot 생성
ax_2 = fig.add_subplot(1,2,2) #두 개의 plot 생성
ax_1.plot(x_1, y_1, c='b')
ax_2.plot(x_2, y_2, c='g')
plt.show()
기타 속성
- color : 흑백, rgb, predefiend color 사용 가능
- ls또는 linestyle로 선 스타일 지정 가능
- pyplot에 title 함수로 figure의 subolot별 입력 가능 (atex 차입의 표현도 가능)
- legend 함수로 범례 표시와, loc 위치 등 속성 지정도 가능
- grid 함수로 보조선을 그을 수 있고, xy축 범위 한계 지정도 가능.
x = range(-100, 100)
y = [x_**2 + x_*2 + 1 for x_ in x]
#color 패러미터로 색 지정 가능. rgb는 그냥 소문자 입력.
#color이나 c 둘 다 가능.
#ls 혹은 linestyle로 선 스타일 지정 : dashed, dotted
#label 두 개 이상의 선일 경우 각 선의 설명
plt.plot(x,y, color = "#000000", ls = "dotted", label = 'line1')
#title 지정
plt.title("(x+1)^2")
#latex 타입의 표현도 가능 ex ) '$y = \\frac{ax+b}{test}$'
#legend로 범례 표현 및 loc 위치 등 속성 지정
#그런데 쓰려면 plot() 안에 label 필요
plt.legend(shadow = True, fancybox = True, loc = "lower right")
#grid : 그래프의 보조선 긋기
plt.grid(True, lw = 0.4, ls = "--", c=".90")
#xlim, ylim xy축 범위 한계 지정
plt.xlim(-200,200) #-200~200까지만 출력
plt.ylim(-200,200)
#저장도 가능
#plt.savefig("test.png", c="a")
#저장하기 전에 show를 하면 파일을 flush를 하기 때문에 메모리 상에 사라짐.
#저장하고 show 하자.
plt.show()import matplotlib.pyplot as plt
import pandas as pd
df = pd.read_csv("phone_data.csv")
def parsedate(date_info) :
import datetime
return date_info[:9]
df["day"] = df["date"].map(parsedate)
result = df.groupby(["network", "day"])["duration"].sum().reset_index()
fig = plt.figure()
fig.set_size_inches(10,10)
plt.style.use("ggplot")
network_type = result['network'].unique().tolist()
ax = []
for i in range(1, 7) :
ax.append(fig.add_subplot(2,3,i))
network_name = network_type[i-1]
plt.title(network_name)
x_1 = result[result["network"] == network_name]["day"]
y_1 = result[result["network"] == network_name]["duration"]
ax[i-1].get_xaxis().set_visible(False)
ax[i-1].plot(x_1, y_1)
그래프 종류
1) 산전도 그래프
- scatter 함수를 사용한다.
- marker: scatter 모양 지정.
- s : 데이터 크기를 지정하고 데이터 크기 비교 가능
import numpy as np
x = np.random.rand(100, 2)
y = np.random.rand(100, 2)
plt.scatter(x[:,0], y[:,1], c="b", marker = "x") #x모양의 청색 점
plt.scatter(y[:,0], x[:,1], c="r", marker = "^") #▲모양의 적색 점
plt.show()
n=50 #크기 지정
x = np.random.rand(n)
y = np.random.rand(n)
colors = np.random.rand(n)
area = np.pi * (15 * np.random.rand(n)) ** 2
plt.scatter(x, y, s= area, c=colors, alpha=0.5)
plt.show()
2) 막대 그래프
data = [[5, 25, 50, 20], [4, 23, 51, 17], [6, 22, 52, 19]]
x = np.arange(4)
plt.bar(x, data[0], color = 'b', width = 0.25)
plt.bar(x + 0.25, data[1], color = 'g', width = 0.25)
plt.bar(x + 0.5, data[2], color = 'r', width = 0.25)
plt.xticks(x+0.25, ("A","B","C","D"))
plt.show()
#위로 쌓기도 가능
data = np.array(data)
color_list = ['b','g','r']
data_label = ["A","B","C"]
x = np.arange(data.shape[1])
for i in range(data.shape[0]) :
plt.bar(x, data[i], bottom = np.sum(data[:i], axis = 0), color = color_list[i], label = data_label[i])
plt.legend()
plt.show()
#양 옆으로도 가능
fst_pop = np.array([1,2,3,4,5])
snd_pop = np.array([5,4,3,2,1])
x = np.arange(5)
plt.barh(x, fst_pop, color='r')
plt.barh(x, -snd_pop, color='b') #-를 붙여줘야 반대방향으로 감.
plt.show()3) 히스토그램
x = np.random.randn(1000)
plt.hist(x, bins = 100) #bins의 갯수만큼의 막대들 출력
plt.show()4) BoxPlot
- 최소값(0%)과 최대값(100%)을 보여주고 25%~75%의 범위를 보여주는 그래프이다.
seaborn
- 통계적 데이터를 시각화할 때 좋다.
- matplotlib에 기본 설정을 추가해 더 쉽게 다룰 수 있게 해주는 툴이다.
- 복잡한 그래프를 간단하게 만들 수 있는 wrapper가 추가됐다.
- 간단한 코드로 예쁜 결과 구현이 가능하다.
- matplotlib과 같은 기본적인 plot인데 손쉬운 설정으로 데이터 산출 가능하다.
- lineplot, scatterplot, countplot 등의 그래프 표현도 가능하다.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
sns.set(style="darkgrid")
tips = sns.load_dataset("tips")
fmri = sns.load_dataset("fmri")
sns.set_style("whitegrid")
#sns.lineplot(x="timepoint", y="signal", data=fmri)
#퍼진 거는 분포
#hue는 해당 칼럼에 따라 다른 결과값을 모두 출력해주는 것.
sns.lineplot(x="timepoint", y="signal", hue="event", data=fmri)
*이 외에도 여러 그래프 존재
- Vilolinplot - bosplot에 distribution을 함께 표현
- Stripplot - scatter와 category 정보를 함께 표현
- Swarmplot - 분포와 함께 scatter를 함께 표현
- Pointplot - 카테고리별로 numeric의 평균, 신뢰구간 표시
- regplot - scatter + 선형함수를 함께 표시
- replot - Numeric 데이터 중심의 분포, 선형 표시
- catplot - 카테고리 데이터 중심의 표시
- FacetGrid - 특정 조건에 따른 다양한 plot을 그리드로 표시
- pairplot - 데이터 간의 상관관계
- Implot - regression 모델과 category 데이터를 함께 표시
seaborn - multiple plots
- 한 개 이상의 여러 종류의 도표를 하나의 plot에 작성하는 법
- axes를 사용해 grid를 나누는 방법이다.
#산전도 그래프
sns.scatterplot(x="total_bill", y="tip", data=tips)
#산전도 그래프와 선 그래프를 함께 출력
sns.regplot(x="total_bill", y="tip", data=tips)#countplot : 카테고리데이터의 갯수 셈
sns.countplot(x= "smoker", data=tips)
#hue 추가하면 카테고리 세분화 가능sns.barplot(x="day", y = "total_bill", data = tips)
#평균 + 분포(선)을 보여줌sns.distplot(tips["total_bill"],bins=10, kde=False)import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
sns.set(style = "white", palette = "muted", color_codes = True)
rs = np.random.RandomState(10)
f, axes = plt.subplots(2, 2, figsize = (7,7), sharex = True)
sns.despine(left = True)
d = rs.normal(size = 100)
sns.displot(d, kde=False, color="b", ax = axes[0, 0])
sns.displot(d, hist=False, rug=True, color="r", ax = axes[0, 1])
sns.displot(d, hist=False, color="g", ked_kws = {"shade" : True}, ax = axes[1, 0])
sns.displot(d, color="m", ax = axes[1, 1])
plt.setp(axes, yticks=[])
plt.tight_layout()
모수 (parameter)
- 통계적 모델링은 적절한 가정 위에서 확률분포를 추정하는 것이 목표이다.
- 이는 기계학습과 통계학이 공통적으로 추구하는 목표이기도 하다.
- 그러나 유한한 개수의 데이터만 관찰해서 모집단의 분포를 정확하게 알아내는 것은 불가능하다. 그렇기에 근사적으로 확률분포를 추정해야 한다.
- 여기서 예측 모형의 목적은 분포를 정확하게 맞추는 것보다 데이터와 추정 방법의 불확실성을 고려해서 위험을 최소화하는 것
- 데이터가 특정 확률분포를 따른다고 선험적으로 (a priori) 가정한 후 그 분포를 결정하는 모수를 추정하는 방법을 모수적 방법론이라 한다.
- 특정 확률분포를 가정하지 않고 데이터에 따라 모델의 구조 및 모수의 개수가 유연하게 바뀐 것을 비모수 방법론이라 한다.
- 기계학습의 많은 방법론은 비모수 방법론에 속한다.
- 참고로 비모수방법론은 모수가 없는 것이 아니라, 모수가 무한히 많거나 모수가 자주 바뀌는 경우이다.
확률분포 가정하기
• 확률분포를 가정하는 방법 : 우선 히스토그램을 통해 모양을 관찰한다
• 데이터가 2개의 값(0 또는 1)만 가지는 경우→베르누이분포
• 데이터가 n개의 이산적인 값을 가지는 경우→카테고리분포
• 데이터가 [0,1] 사이에서 값을 가지는 경우→베타분포
• 데이터가 0이상의 값을 가지는 경우→감마분포, 로그정규분포등
• 데이터가 전체에서 값을 가지는 경우→정규분포, 라플라스분포등
• 기계적으로 확률분포를 가정해서는 안되며, 데이터를 생성하는 원리를 먼저 고려하는 것이 원칙이다
*각 분포마다 검정하는 방법들이 있으므로 모수를 추정한 후 반드시 검정해야 한다.
데이터의 모수 추정
- 데이터의 확률분포를 가정했다면 모수 추정이 가능하다.
- 정규분포의 모수는 평균과 분산이다.
- 통계학의 확률분포를 표집분포 (Sampling distribution)이라 부르며, 표본평균의 표집분포는 n이 커질수록 정규분포에 가까워진다.
- 이를 중심극한정리라 부르며 모집단의 분포가 정규분포를 따르지 않아도 성립한다.

최대가능도 (Maximum likelihood estimation, MLE)
- 표본평균이나 표본분산은 중요한 통계랑이지만 확률분포마다 사용하는 모수가 달라 적절한 통계량이 달라진다.
- 이론적으로 가장 가능성이 높은 모수를 추정하는 방법으로 최대가능도 추정법이 있다.
- 가능도 함수는 모수를 따르는 분포가 x를 관찰할 가능성을 뜻한다.
- 참고로 이를 확률로 해석해서는 안된다.
- MLE는 데이터 집합 X가 독립적으로 추출되었을 경우 로그가능도를 최적화 한다.

로그가능도
- 로그가능도를 최적화 하는 모수는 가능도를 최적화하는 MLE가 된다.
- 데이터의 숫자가 적으면 상관없지만 데이터의 숫자가 많으면 컴퓨터의 정확도로는 가능도 계산이 불가능하다.
- 데이터가 독립일 경우 로그 사용시 가능도의 곱셈을 로그가능도의 덧셈으로 바꿀 수 있고, 컴퓨터 연산이 가능해진다.
- 경사하강법으로 가능도를 최적화할 때 미분 연산을 사용하는데, 로그가능도를 사용하면 연산량이 o(n^2)에서 o(n)으로 줄어든다.
- 대게의 손실함수의 경우 경사하강법을 사용하므로 음의 로그 가능도를 최적화한다.
*경사하강법으로 목적식을 최소화 => 음의 로그 가능도로 최적화

최대가능도 추정법 : 정규분포
- 정규분포를 따르는 확률변수 x로부터 독립적인 표본을 얻었을 때 최대가능도 추정법을 이용하여 모수를 추정하면?

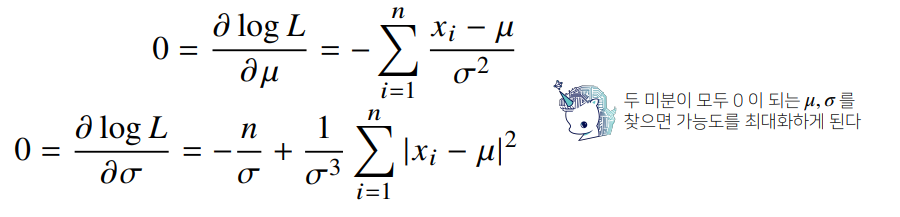

최대가능도 추정법 : 카테고리 분포
- 카테고리 분포 Multinoulli (x : p1, ... pn)을 따르는 확률분포 X로부터 독립적인 표본을 얻었다면 최대가능도 추정법으로 모수를 추정하면?



딥러닝에서 최대가능도 추정
- 최대가능도 추정법을 이용해 기계학습 모델을 학습할 수 있다.
- 딥러닝 모델의 가중치를 θ = (W(1), …, W(L)) 라고 표기했을 때 분류 문제에서 소프트맥스 벡터는 카테고리분포의 모수 (p1 ~ pk)를 모델링한다.
- 원핫 벡터로 표현한 정답레이블 y = (y1~yk)를 관찰데이터로 이용해 확률분포인 소프트맥스 벡터의 로그 가능도를 최적화할 수 있다.

확률분포의 거리 구하기
- 기계학습에서 사용되는 손실함수들은 모델이 학습하는 확률분포와 데이터에서 관찰되는 확률분포의 거리를 통해 유도한다.
- 데이터공간에 두 개의 확률분포 P(x), Q(x)가 있을 경우 두 확률분포의 거리를 계산할 때는 다음의 함수들을 사용한다.
- 총 변동 거리, 쿨백-라이블러 발산, 바슈타인 거리
쿨백-라이블러 발산

- 피어세션 회의 내용
어제 학습한 것을 다시 학습하는 시간을 가졌다.
Further Question에서 코드에 대해 질문하여, 해당 코드가 베르누이 분포임을 알았다.
1.
교차 엔트로피 → negative log likelihood 와 같은 형태.
2.
분산 및 불확실성 최소화
분산이 크면 정보량이 많다로 해석할 수 있다.
→ 정보량이 많으면 엔트로피가 그만큼 크다고 할 수 있다. (엔트로피는 정보량의 기댓값)
→ 분산을 최소화 시키는 것이 엔트로피를 최소화 시키는 것으로 생각할 수 있다.
3. 확률, 확률분포
확률분포 : 확률과 확률변수의 집합 비슷한 개념
4. 분류문제에서의 softmax함수를 이용해 패턴을 통해 조건부확률을 계산.
5. 분류는 여러 레이블 중 하나를 예측(이산적.) 회귀는 연속적인 실수를 예측(연속적)
- 해야할 일
Furthur Question
1. 확률과 가능도의 차이?
| 확률 | 가능도 | |
| 개념적 | 주어진 확률분포에서 해당 관측값이 나올 확률 | 주어진 관측값이 어떤 확률분포에서 어느정도의 확률로 나타나는지 확률 |
| 수식 | P(관측값 | 확률분포) | P(확률분포 | 관측값) |
| 확률밀도함수 | 함수에서 영역으로 관측된다 ex) 캐리어 무게가 20~30kg일 확률 |
함수에서 한 점으로 관측된다. ex) 캐리어 무게가 30일 경우 가능도 |
2. 확률 대신 가능도를 사용했을 때의 이점
표본평균과 표본분산을 구할 때 확률분포마다 사용하는 모수가 다르기에 적절한 통계량이 다르다. 그래서 모수를 추정해야 하는데, 가능도를 사용하는 것이 가장 가능성이 높다.
3. 다음 코드는 어떤 확률분포를 나타내는 것인가?

3-1. 해당 확률분포에서 변수 세타가 의미할 수 있는 것은?
theta는 어떤 사건이 일어날 확률
위의 코드는 0~1 사이의 가능성을 가진 theta가 10번의 사건 중 3번 일어날 확률에 대한 코드이다.
'BOOSTCAMP AI TECH > 2주차_AI를 위한 수학' 카테고리의 다른 글
| [BOOSTCAMP AI TECH] 9일차_Pandas 2, 확률론 (0) | 2021.01.28 |
|---|---|
| [BOOSTCAMP AI TECH] 8일차_Pandas / 딥러닝 학습방법 이해하기 (0) | 2021.01.27 |
| [BOOSTCAMP AI TECH] 7일차_경사하강법 (0) | 2021.01.26 |
| [BOOSTCAMP AI TECH] 6일차_Numpy/벡터/행렬 (0) | 2021.01.25 |



