대학생때부터 취업 직전까지 많이 듣고 많이 공부한 알고리즘 중 하나는 당연 트리이고, 그 중 이진트리를 기초로 생각하고 배운 적이 있다.
한창 취준하며 코테를 공부하던 때에는 과장해서 말하자면 이진트리는 굳이 생각이라는 것을 거치지 않고도 단어만 듣고 코드가 줄줄 써지는 정도였다.
하지만 너무 기초라고 생각했고, 취업 이후에는 이 구현 방법 자체를 머리속에서 지우고 살았다. 자기변명을 해보자면, 이진 트리를 굳이 실무에서 적용할 일이 없었고, 또 지난 여러 기업의 코딩 테스트를 응시하며 이진 트리가 나온 적은 한 번도 존재하지 않았었기 때문이다.
*물론 많은 회사의 코딩테스트에 응시했던 것은 아니므로, 언제 어디서 등장할 지는 모른다. 이 사실을 상기하지 못한 것에 대한 변명일 뿐이다.
그렇게 살던 중 오늘 한 회사의 코딩 테스트에 응시했고, 이진트리 구현 문제가 출제되었다.
그 문제를 보자마자 바로 생각이 들었다.
"엥? 이진트리? 뭐 이런 쉬운 걸 문제로 내고 그러신대? 시험 빠르게 끝낼 수 있겠다!"
그리고 타이핑을 하려고 손가락을 움직이려던 찰나, 이런 생각이 뒤를 이었다.
"어... 그런데 이거 어떻게 구현하는 거더라..?"
결론부터 말하자면 코테는 망했다. 기초중의 기초라고 생각했지만 구현 방법이 생각나지 않는 이진트리의 등장에 머리속이 새하얘졌고, 스스로 생각하기에 나의 가장 큰 단점인 "한 번 당황하면 그 이후로 아무것도 못하는" 버릇이 도졌다. 그렇게 벙쪄서 시간만 잡아먹다가 결국 이진 트리도 구현하지 못했고, 다음 문제도 시간이 부족해 구현할 시간조차 없었다.
물론 아직 완전하게 탈락 메일이 온 것은 아니므로 희망을 놓기는 이르지만, 기초중의 기초라고 생각했던 것조차 곧바로 생각하지 못하고 이로 인해 시험을 망쳐버린 스스로가 한심하게 느껴졌다.
그렇다고 계속 자책만 하고 있을 수는 없기에, 비록 소 잃고 외양간 고치기일 지언정 다시는 같은 실수를 하지 않도록 오늘은 이진 트리에 대해 공부하고, 오늘 못짠 코드를 한 번 구현해볼까 한다.
트리 (Tree)
트리는 계층적인 데이터 구조로, 여러 노드들이 부모-자식 관계로 이루어진다.
그림을 그려보면 다음과 같이 구성될 수 있다.
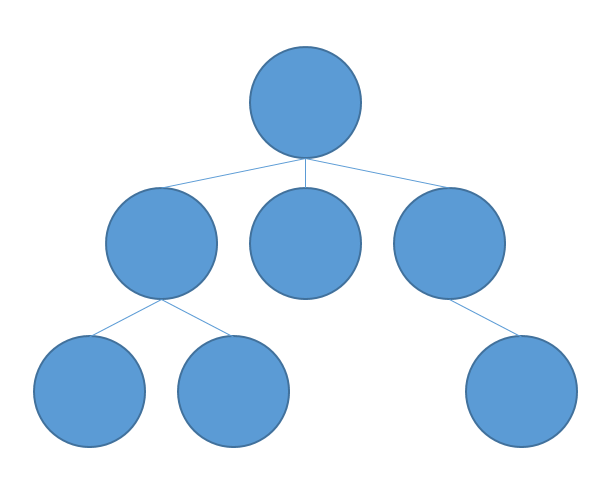
트리는 다음과 같은 특징을 가진다.
- 계층적 구조로 이루어진다.
- 각 트리는 하나의 루트 노드를 가진다.
- 순환 구조가 없어, 어떤 경로를 통하더라도 자식에서 부모 노드로 돌아갈 수는 없다.
- 각 노드는 유일한 식별자를 가진다.
그리고 트리에서 사용되는 용어는 다음과 같다.
- node : 위 그림에서 하나하나의 파란 동그라미로, 데이터를 저장하는 단위
- edge : 노드들을 연결하는 선
- root : 최상위 노드, 즉 가장 위에 있는 노드
- leaf : 트리의 끝 노드, 즉 가장 아래에 있는 노드들
- parent : 다른 노드의 상위에 있는 노드
- child : 다른 노드의 하위에 있는 노드
- sibling : 같은 부모를 가진 노드
- subtree : 트리 내의 어떤 노드와 그 자손 노드로 이루어진 트리
- depth : 트리의 높이로, root부터 leaf까지의 간선의 길이
순회
트리는 탐색 방법에 따라 전위순회, 중위순회, 후위 순회로 나눌 수 있다. 그리고 각 순회의 개념은 아래와 같다.
- 전위순회 (Preorder) : 위 > 왼쪽 > 오른쪽 순
- 중위순회 (InOrder) : 왼쪽 > 위 > 오른쪽 순
- 후위순회 (PostOrder) : 왼쪽 > 오른쪽 > 위 순
예시를 들자면 아래와 같이 할 수 있겠다.

- 전위순회 : 1 2 4 8 9 5 3 6 7
- 중위순회 : 8 4 9 2 5 1 6 3 7
- 후위순회 : 8 9 4 5 2 6 7 3 1
이진 트리 (Binary Tree)
트리의 종류는 다양하다. 이진 트리, 이진 검색 트리, AVL 트리, B-트리, 트라이 등. 그렇다면 오늘 주제인 이진 트리는 어떤 트리일까?
개념 자체는 간단하다. 이진 트리란 자식 노드가 최대 두 개로 구성된 노드들로 구성된 트리이다.
그림으로 따지면 아래와 같다.

이진 트리 구현
개념 자체는 별게 없다. 그저 자식 노드의 수가 최대 두 개까지만 허용되는 트리일 뿐이다.
그렇다면 구현을 한 번 해보자.
구현은 left가 비었으면 left에 먼저 삽입하도록 구현해보았다.
우선 여느 트리들이 그렇듯, 일단 Node Class가 필요하다.
static class Node {
int data;;
Node left;
Node right;
Node(int data) {
this.data = data;
}
}
그리고 Node를 종합하는 Tree 클래스를 생성한다.
static class BinaryTree {
Node root;
/**
* 데이이터 입력
* @param data
*/
public void insert(int data) {
if(root == null){
// 아직 root가 입력되지 않음.
root = new Node(data);
}
else {
Queue<Node> queue = new LinkedList<>();
queue.add(root);
// 큐를 통해 트리 채우기
while(!queue.isEmpty()) {
Node tmpNode = queue.poll();
if(tmpNode.left == null) {
// left가 비어있으면 삽입
tmpNode.left = new Node(data);
break;
}
else if(tmpNode.right == null) {
// right가 비어있으면 삽입
tmpNode.right = new Node(data);
break;
}
else {
// 둘 다 차있으면, left > right 순으로 다시 한 번 순차 검색
queue.add(tmpNode.left);
queue.add(tmpNode.right);
}
}
}
}
/**
* 전위순회
* @return
*/
public String preOrder() {
StringBuffer result = new StringBuffer();
preOrder(root, result);
return result.toString();
}
public void preOrder(Node node, StringBuffer result) {
if(node == null) {
return;
}
// 위 > 왼 > 오 순
result.append(node.data + " ");
preOrder(node.left, result);
preOrder(node.right, result);
}
/**
* 중위순회
* @return
*/
public String inOrder() {
StringBuffer result = new StringBuffer();
inOrder(root, result);
return result.toString();
}
public void inOrder(Node node, StringBuffer result) {
if(node == null) {
return;
}
// 왼 > 위 > 오 순
inOrder(node.left, result);
result.append(node.data + " ");
inOrder(node.right, result);
}
/**
* 후위순호
* @return
*/
public String postOrder() {
StringBuffer result = new StringBuffer();
postOrder(root, result);
return result.toString();
}
public void postOrder(Node node, StringBuffer result) {
if(node == null) {
return;
}
// 왼 > 오 > 위 순
postOrder(node.left, result);
postOrder(node.right, result);
result.append(node.data + " ");
}
}
마지막으로 테스트를 위한 main 클래스를 생성했다.
public static void main(String[] args) {
int[] testOne = new int[] {1, 2, 3, 4, 5, 6, 7, 8, 9};
int[] testTwo = new int[] {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13};
int[] testThree = new int[] {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20};
// 1번 테스트
System.out.println("\n== testOne ==");
BinaryTree testOneTree = new BinaryTree();
for(int num : testOne) {
testOneTree.insert(num);
}
System.out.println("preOrder : " + testOneTree.preOrder());
System.out.println("inOrder : " + testOneTree.inOrder());
System.out.println("postOrder : " + testOneTree.postOrder());
// 2번 테스트
System.out.println("\n== testTwo ==");
BinaryTree testTwoTree = new BinaryTree();
for(int num : testTwo) {
testTwoTree.insert(num);
}
System.out.println("preOrder : " + testTwoTree.preOrder());
System.out.println("inOrder : " + testTwoTree.inOrder());
System.out.println("postOrder : " + testTwoTree.postOrder());
// 3번 테스트
System.out.println("\n== testThree ==");
BinaryTree testThreeTree = new BinaryTree();
for(int num : testThree) {
testThreeTree.insert(num);
}
System.out.println("preOrder : " + testThreeTree.preOrder());
System.out.println("inOrder : " + testThreeTree.inOrder());
System.out.println("postOrder : " + testThreeTree.postOrder());
}
이제 테스트를 해보자.
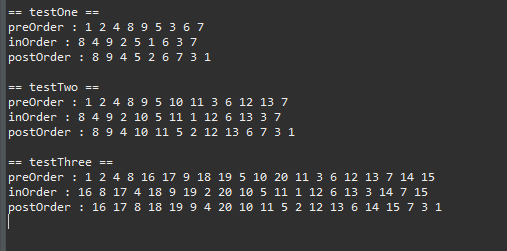
정상적으로 구동함을 확인할 수 있다.
그리고 모든 소스 코드는 아래에 적어두었다.
package baekjoon;
import java.util.LinkedList;
import java.util.Queue;
public class Main {
static class Node {
int data;;
Node left;
Node right;
Node(int data) {
this.data = data;
}
}
static class BinaryTree {
Node root;
/**
* 데이이터 입력
* @param data
*/
public void insert(int data) {
if(root == null){
// 아직 root가 입력되지 않음.
root = new Node(data);
}
else {
Queue<Node> queue = new LinkedList<>();
queue.add(root);
// 큐를 통해 트리 채우기
while(!queue.isEmpty()) {
Node tmpNode = queue.poll();
if(tmpNode.left == null) {
// left가 비어있으면 삽입
tmpNode.left = new Node(data);
break;
}
else if(tmpNode.right == null) {
// right가 비어있으면 삽입
tmpNode.right = new Node(data);
break;
}
else {
// 둘 다 차있으면, left > right 순으로 다시 한 번 순차 검색
queue.add(tmpNode.left);
queue.add(tmpNode.right);
}
}
}
}
/**
* 전위순회
* @return
*/
public String preOrder() {
StringBuffer result = new StringBuffer();
preOrder(root, result);
return result.toString();
}
public void preOrder(Node node, StringBuffer result) {
if(node == null) {
return;
}
// 위 > 왼 > 오 순
result.append(node.data + " ");
preOrder(node.left, result);
preOrder(node.right, result);
}
/**
* 중위순회
* @return
*/
public String inOrder() {
StringBuffer result = new StringBuffer();
inOrder(root, result);
return result.toString();
}
public void inOrder(Node node, StringBuffer result) {
if(node == null) {
return;
}
// 왼 > 위 > 오 순
inOrder(node.left, result);
result.append(node.data + " ");
inOrder(node.right, result);
}
/**
* 후위순호
* @return
*/
public String postOrder() {
StringBuffer result = new StringBuffer();
postOrder(root, result);
return result.toString();
}
public void postOrder(Node node, StringBuffer result) {
if(node == null) {
return;
}
// 왼 > 오 > 위 순
postOrder(node.left, result);
postOrder(node.right, result);
result.append(node.data + " ");
}
}
public static void main(String[] args) {
int[] testOne = new int[] {1, 2, 3, 4, 5, 6, 7, 8, 9};
int[] testTwo = new int[] {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13};
int[] testThree = new int[] {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20};
// 1번 테스트
System.out.println("\n== testOne ==");
BinaryTree testOneTree = new BinaryTree();
for(int num : testOne) {
testOneTree.insert(num);
}
System.out.println("preOrder : " + testOneTree.preOrder());
System.out.println("inOrder : " + testOneTree.inOrder());
System.out.println("postOrder : " + testOneTree.postOrder());
// 2번 테스트
System.out.println("\n== testTwo ==");
BinaryTree testTwoTree = new BinaryTree();
for(int num : testTwo) {
testTwoTree.insert(num);
}
System.out.println("preOrder : " + testTwoTree.preOrder());
System.out.println("inOrder : " + testTwoTree.inOrder());
System.out.println("postOrder : " + testTwoTree.postOrder());
// 3번 테스트
System.out.println("\n== testThree ==");
BinaryTree testThreeTree = new BinaryTree();
for(int num : testThree) {
testThreeTree.insert(num);
}
System.out.println("preOrder : " + testThreeTree.preOrder());
System.out.println("inOrder : " + testThreeTree.inOrder());
System.out.println("postOrder : " + testThreeTree.postOrder());
}
}
'IT 지식 > 알고리즘' 카테고리의 다른 글
| [알고리즘] DP (0) | 2021.10.26 |
|---|---|
| [알고리즘] BFS와 DFS (0) | 2021.10.26 |
| [알고리즘] 정렬 알고리즘 (0) | 2021.04.05 |


