728x90
반응형
위키독스
온라인 책을 제작 공유하는 플랫폼 서비스
wikidocs.net
*해당 글은 학습을 목적으로 위의 포스팅 내용 중 일부 내용만을 요약하여 작성한 포스팅입니다.
상세한 내용 및 전체 내용 확인은 위의 링크에서 확인하실 수 있습니다.
원 핫 인코딩 (One-Hot Encoding)
- 범주형 데이터를 처리할 때 레이블을 표현하는 방법
- 선택해야 하는 선택지의 개수만큼 차원을 가지며, 각 선택지의 인덱스에 해당하는 원소는 1, 나머지는 0으로 채우는 표현 방법
- 원 핫 인코딩으로 표현한 벡터를 원 핫 벡터라고 한다.
다중 클래스 분류 (Multi-class Classification)
- 둘 중 하나만을 정하는 이진 분류와 달리 세 개 이상의 선택지 중 답을 고르는 문제
- 다중 클래스 분류를 위해 소프트맥스 회귀가 사용된다.
- 소프트맥스 회귀는 확률의 총 합이 1이 되는 아이디어를 다중 클래스 분류 문제에 적용한다.
- 선택지의 개수만큼의 차원을 가지는 벡터를 만들고, 해당 벡터가 모든 원소의 합이 1이 되도록 값을 변화시킨다.
- 이러한 변화를 만들어주는 함수를 소프트맥스 함수라고 부른다.
소프트맥스 함수 (Softmax Function)


- p(i)는 i번째 클래스가 정답일 확률
- z(i)는 i번째 원소
소프트맥스 회귀의 비용 함수
- 이진 분류에서는 바이너리 크로스 엔트로피를 사용했다.
- 소프트맥스 회귀에는 크로스 엔트로피를 사용한다.
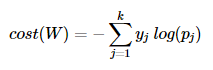
- y는 실제값
- k는 클래스 갯수
- y(j)는 실제값 원-핫 벡터의 j번째 인덱스
- p(j)는 샘플 데이터가 j번째 클래스일 확률.
원 핫 인코딩 vs 소프트맥스
- 원 핫 인코딩은 반드시 모 아니면 도의 결과값을 가졌다.
- 선택한 선택지는 1, 나머지는 모두 0이었기 때문이다.
- 예를들어 한 사진이 개일까, 고양이일까 분류하는 모델이 있을 때 원 핫 인코딩은 반드시 해당 사진은 무조건 개 아니면 고양이 임을 표시한다.
- 하지만 그에 반해 소프트맥스는 확률값을 계산한다.
- 위의 예시로 들면, 개일 확률은 90%, 고양이일 확률은 10%로 계산될 수 있다.
- 이러한 방식은 모 아니면 도가 아닌 확률을 계산하게 해주어, 보다 유연한 예측을 가능하게 해주어, 다른 예측이 나올 수 있는 경우에 대한 정보를 전해줄 수 있다.
코드 (MNIST Classification)
import torch
import torchvision.datasets as dsets
import torchvision.transforms as transforms
from torch.utils.data import DataLoader
import torch.nn as nn
import torch.nn.functional as F
import matplotlib.pyplot as plt
import random
from tqdm.notebook import tqdm
USE_CUDA = torch.cuda.is_available() # GPU를 사용가능하면 True, 아니라면 False를 리턴
device = torch.device("cuda" if USE_CUDA else "cpu") # GPU 사용 가능하면 사용하고 아니면 CPU 사용
print(device)
# 랜덤 시드 고정
random.seed(777)
torch.manual_seed(777)
if device == 'cuda':
torch.cuda.manual_seed_all(777)
# MNIST dataset
mnist_train = dsets.MNIST(root='MNIST_data/',
train=True,
transform=transforms.ToTensor(),
download=True)
mnist_test = dsets.MNIST(root='MNIST_data/',
train=False,
transform=transforms.ToTensor(),
download=True)
data_loader = DataLoader(mnist_train, batch_size=100, shuffle=True, drop_last=True) # drop_last : 마지막 배치 버리기
# 마지막 배치 ? => 1000개의 데이터를 128 배치로 나누면 마지막 배치는 104개인데,
# 다른 미니배치보다 작은 미ㅣ니 배치를 사용하면 마지막 배치가 상대적으로 과대 평가될 수 있음.
# 그래서 버려준다.
class DNNModel(nn.Module) :
def __init__(self, device) :
super().__init__()
self.linear1 = nn.Linear(28*28, 64).to(device)
self.linear2 = nn.Linear(64, 10).to(device)
def forward(self, x) :
output = self.linear1(x)
output = F.relu(output)
output = self.linear2(output)
output = F.softmax(output)
return output
model = DNNModel(device)
criterion = nn.CrossEntropyLoss().to(device) #내부적으로 softmax 함수 포함 : softmax 따로 쓸 필요가 없음.
optimizer = torch.optim.SGD(model.parameters(), lr=0.01) #weight_decay 파라미터 포함시 가중치 규제
n_epoch = 20
for epoch in range(n_epoch) :
avg_cost = 0
avg_acc = 0
total_data = 100 * len(data_loader)
total_batch = len(data_loader)
for x, y in tqdm(data_loader) :
x = x.view(-1, 28 * 28).to(device) #100, 1, 28, 28 => 100, 784(28*28)
y = y.to(device)
predict = model(x)
cost = criterion(predict, y)
optimizer.zero_grad()
cost.backward()
optimizer.step()
avg_cost += cost / total_batch
correct_prediction = torch.argmax(predict, 1) == y # [True, Flase, True ...]
correct_prediction = correct_prediction.sum()
avg_acc += correct_prediction
avg_acc = avg_acc.item()
avg_acc /= total_data
print('Epoch {} : cost {:.5f}, acc {:.5f}'.format(epoch+1, avg_cost, avg_acc))
if avg_acc > 0.95 :
print('early stop')
break
#테스트 데이터로 테스트
with torch.no_grad() : #no_grad()시 경사도 계산 안함
x_test = mnist_test.test_data.view(-1, 28*28).float().to(device)
y_test = mnist_test.test_labels.to(device)
predict = model(x_test)
correct_prediction = torch.argmax(predict, 1) == y_test #이러면 [True, False, True, True, ... ,False] 이렇게 나옴.
accuracy = correct_prediction.float().mean()
print('accuracy : ', accuracy.item())
# MNIST 테스트 데이터에서 무작위로 하나를 뽑아서 예측을 해본다
r = random.randint(0, len(mnist_test) - 1)
X_single_data = mnist_test.test_data[r:r + 1].view(-1, 28 * 28).float().to(device)
Y_single_data = mnist_test.test_labels[r:r + 1].to(device)
print('Label: ', Y_single_data.item())
single_prediction = model(X_single_data)
print('Prediction: ', torch.argmax(single_prediction, 1).item())
plt.imshow(mnist_test.test_data[r:r + 1].view(28, 28), cmap='Greys', interpolation='nearest')
plt.show()
728x90
반응형
'IT 도서 > Pytorch로 시작하는 딥 러닝 입문' 카테고리의 다른 글
| 06. 합성곱 신경망 (Convolution Neural Network) (0) | 2021.03.02 |
|---|---|
| 05. 인공 신경망 (Artificial Neural Network) (0) | 2021.03.02 |
| 03. 로지스틱 회귀 (Logistic Regression) (0) | 2021.03.01 |
| 02. 선형 회귀 (Linear Regression) (0) | 2021.03.01 |
| 01. 파이토치 기초 (Pytorch Basic) (0) | 2021.03.01 |


