[BOOSTCAMP AI TECH] 21일차_그래프 이론 기초 & 그래프 패턴

728x90

강의 목록

- 그래프란 무엇이고 왜 중요할까?

- 실제 그래프는 어떻게 생겼을까?

요약

강의

AI를 위한 그래프를 배우기 위해 기초적인 지식들을 학습했다.

피어세션

지난 주 학습을 복습하는 시간을 가졌다.

학습정리

그래프 (네트워크)

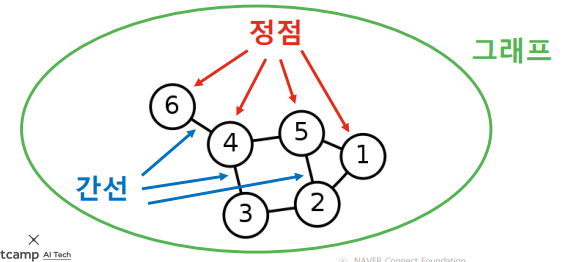
정점 집합과 간선 집합으로 이루어진 수학적 구조
하나의 간선은 두 개의 정점으로 연결한다.
모든 정점 쌍이 반드시 간선으로 직접 연결되는 것은 아니다.

정점 = Vertex, Node / 간선 = Edge, Link

그래프가 중요한 이유?

우리 주변에는 많은 복잡계 (Complex System)가 존재한다. 사회, 통신 시스템, 정보, 지식, 뇌, 신체 역시 모두 복잡계이다.
이러한 복잡계는 구성 요소 간 복잡한 상호작용을 한다는 특성을 가지고 있다.
그래프는 복잡계를 표현하고 분석하기 위한 언어이다.
복잡계를 이해하고, 정확한 예측을 위해서는 그래프에 대한 이해가 반드시 필요하다.

그래프 관련 인공지능 문제

-정점 분류 문제

트위터에서의 리트윗 관계를 분석하여 각 사용자의 정치적 성향을 알 수 있을까?
단백질의 상호작용을 분석하여 단백질의 역할을 알아낼 수 있을까?

-연결 예측 문제

페이스북 소셜 네트워크는 어떻게 진화할까?

-추천 문제

각자에게 필요한 물건은 무엇일까?
어떤 물건을 구매해야 만족도가 높을까?

-군집 문석 문제

연결 관계로부터 사회적 무리 (Social Circle)을 찾아낼 수 있을까?

-랭킹 및 정보 검색 문제

웹 이라는 거대한 그래프로부터 어떻게 중요한 웹페이지를 찾아낼 수 있을까?

-정보 전파 및 바이럴 마케팅 문제

정보는 네트워크를 통해 어떻게 전달될까?
어떻게 정보 전달을 최대화 할 수 있을까?

이번 주차에서는 위의 문제들을 해결하는 인공지능 기술의 직관적인 방법론을 학습할 것이다.

또한 일부 그래프 신경망 등 신기술도 소개할 예정이다.

그래프 관련 필수 기초 개념

그래프의 유형 및 분류

1) 방향이 없는 그래프 vs 방향이 있는 그래프 (Undirected Graph vs Directed Graph)

인용 그래프의 경우, 인용을 하는 논문과 당하는 논문이 존재한다. 즉, 관계가 동등하지 않다.
이런 경우 인용을 하는 논문은 인용을 당하는 논문에 방향을 갖는다.
즉 관계가 동등하면 간선에 방향이 없고, 관계가 존재하면 방향이 존재한다.

2) 가중치가 없는 그래프 vs 가중치가 있는 그래프 (Unweighted Grapg vs Weighted Graph)

전화 그래프의 경우 몇 번 전화를 주고 받았는지가 가중치가 된다.
간선에 숫자를 부여할 필요가 없는 경우, 혹은 그 숫자가 큰 의미가 없는 경우 간선에 숫자를 표시하지 않고, 이는 가중치가 없는 그래프가 된다.
간선에 가중치가 없다고 판단하는 것은 지극히 주관적일 수 있다.

3) 동종 그래프 vs 이종 그래프 (Unpartite Graph vs Bipartite Graph)

전자 상거래의 경우, 사람과 물건 사이에만 간선이 존재할 수 있다.
영화 출연 그래프의 경우에도 배우, 영화를 종류로 나누어 각 배우별 출연 영화들을 연결할 수 있다.
이종 그래프는 같은 종류의 정점 사이에서는 간선 연결이 불가능하다.

방향이 없는 그래프, 가중치가 있는 그래프, 이종 그래프

그래프의 정점과 집합

그래프는 정점들의 집합과 간선들의 집합으로 이루어진다.
보통 정점들의 집합을 V, 간선들의 집합을 E로 표현하며, 그래프를 G = (V,E)로 표현한다.
정점의 이웃은 그 정점과 연결된 다른 정점을 의미한다.
정점 v의 이웃들의 집합을 보통 N(v) 혹은 𝑵𝒗로 적는다.
ex) N(1) = {2,5} #1번 정점에 2, 5번 정점이 연결되어 있다. (이웃들의 집합)
방향성이 있는 그래프에서는 나가는 이웃과 들어오는 이웃을 구분한다. 나가는 이웃 (Out-Neighbor)의 집합을 보통 𝑵𝒐ut(v) 라고 적는다. 들어오는 이웃 (In-Neighbor)의 집합을 보통 𝑵in(v) 라고 적는다.
ex) 𝑵in(1) = {5}, 𝑵𝒐ut(1)={2} #5에서 1로 들어오고, 1에서 2로 나간다.

NetworkX

그래프를 생성, 변경, 시각화하고 그 구조와 변화를 살펴볼 수 있는 파이썬 라이브러리
추가로 Snap.py라는 라이브러리도 자주 활용된다.
NetworkX의 경우 사용이 편리하지만 속도가 빠르고, Snap.py의 경우 사용이 불편하지만 속도가 빠르다.
가능하면 둘 다 아는 것이 좋다.

*NetworkX : networkx.org/documentation/stable/index.html

*Snap.py : snap.stanford.edu/snappy/

NerworkX 기본 사용법

import networkx as nx #networkx import
import numpy as np
import matplotlib.pyplot as plt

#그래프 선언
print('### Graph Init ###')
print('# G : 방향성 X #')
print('# DiG : 방향성 O #')
G = nx.Graph() #방향성이 없는 그래프
DiG = nx.DiGraph() #방향성이 있는 그래프


#노드 하나 추가
print('### Add Node to G ###')
print('# Add Node 1 to G #')
G.add_node(1) #정점 1 추가
print('Nodes in G :', G.number_of_nodes(), 'Graph :', G.nodes, '\n')


#노드 여러 개 추가
print('# Add Vertex 2~10 to G #')
for i in range(1, 11) : G.add_node(i)
print('Nodes in G :', G.number_of_nodes(), 'Graph :', G.nodes, '\n')


#간선 하나 추가
print('### Add Edge to G ###')
print('# Add Edg (1,2) to G #')
G.add_edge(1,2)
print('Graph :', G.edges, '\n')


#간선 여러 개 추가
print('# Add Edg (1,i) for i = 2~10 to G #')
for i in range(2, 11) : G.add_edge(1,i)
print('Graph :', G.edges, '\n')


#그래프 시각화
#정점의 위치 결정
pos = nx.spring_layout(G)
#정점의 색과 크기를 지정해 출력
im = nx.draw_networkx_nodes(G, pos, node_color = "red", node_size = 100)
#간선 출력
nx.draw_networkx_edges(G, pos)
#각 정점의 라벨 출력
nx.draw_networkx_labels(G, pos, font_size = 15, font_color = "black")
plt.show()

그래프의 표현 및 저장

1) 간선 리스트 (Edge List)

간선 리스트의 경우에는 그래프를 단순하게 표현할 수 있지만, 사용 측면에서는 조금 비효율적이다.
ex) 없는 간선을 찾는 경우 전부 탐색해야 없음을 알 수 있다.

2) 인접 리스트 (Adjacent list)

특정 간선 검색시 시작점의 리스트만 확인하면 되기 때문에 간선 리스트보다 효율적이다.

3) 인접 행렬 (Adjacency Matrix)

NetworkX를 활용한 그래프 표현 및 저장

#인접 리스트로 저장
list = nx.to_dict_of_lists(G)
print(list)

#간선 리스트로 저장
list = nx.to_edgelist(G)
print(list)

#인접 행렬(일반 행렬)로 저장
list = nx.to_numpy_array(G)
print(list)


#인접 행렬(희소 행렬)로 저장
list = nx.to_scipy_sparse_matrix(G)
print(list)

실제 그래프 vs 랜덤 그래프

실제 그래프 : 다양한 복잡계로부터 얻어진 그래프 ex) 소셜 네트워크, 구매 내역, 인터넷, 뇌 등
랜덤 그래프 : 확률적 과정을 통해 생성한 그래프

에르되스-레니 랜덤 그래프

임의의 두 정점 사이에 간선이 존재하는지 여부를 동일한 확률 분포에 의해 결정한다.
에르되스-레니 랜덤 그래프 G(n, p)는

n개의 정점을 가진다.
임의의 두 정점 사이에 간선이 존재할 확률은 p이다.
정점 간의 연결은 서로 독립적이다.

ex) G(3, 0.3)에 의해 생성될 수 있는 그래프와 각각의 확률은?

작은 세상 효과 (Small-world Effect)

정점 u와 v 사이의 경로(Path)는 아래의 조건을 만족하는 정점들의 순열(Sequence)이다.

u에서 시작해 v에서 끝나야 한다.
순열에서 연속된 정점은 간선으로 연결되어 있어야 한다.

경로의 길이는 경로 상에 놓이는 간선의 수로 정의된다.
정점 u와 v 사이의 거리(Distance)는 u와 v 사이의 최단 경로의 길이이다.
그래프의 지름은 정점 간 최단 경로의 길이인 거리의 최댓값이다.

*여섯 단계 분리 실험 (Six Degrees of Separation)

미국의 사회학자 스탠리 밀그램에 의해 1960년대에 수행된 실험
오하마와 위치타에서 500명의 사람을 선정해 보스턴에 있는 한 사람에게 편지를 전달한 실험
단, 지인을 통해서만 전달해야 한다.
목적지에 도착하기 까지 평균적으로 6단계의 지인을 거쳤다.

여섯 단계 분리 실험은 6단계의 평균 거리를 가지고 있고, 실제 데이터인 MSN 메신저 데이터는 평균 거리가 6이다. (거대 연결 구조 기준)
즉, 아무 연관이 없는 사람이라도 6~7다리만 거치면 서로 연관이 있는 사람이라는 의미이다.
이렇듯 네트워크 자체는 매우 방대하나, 몇 단계만 거치면 서로 연결되어 있는 효과를 작은 세상 효과라고 한다.
ex) 사돈의 팔촌

작은 세상 효과는 높은 확률로 랜덤 그래프에도 존재한다.
하지만 모든 그래프에서 작은 세상 효과가 존재하는 것은 아니다.
체인, 사이클, 격자 그래프에는 작은 세상 효과가 존재하지 않는다.
위의 그래프들에는 각자 거리가 먼 노드들이 존재하는데, 그래프가 커질수록 노드간의 거리가 커지기 때문.

연결성이 두터운 꼬리 분포

정점의 연결성은 그 정점과 연결된 간선의 수를 의미한다.
다른 말로 연결성은 해당 정점의 이웃들의 수와 같다.
정점의 나가는 연결성은 그 정점에서 나가는 간선의 수이다.
정점 v의 나가는 연결성은 𝒅𝒐ut(𝒗) 혹은 |𝑵𝒐ut(𝒗)| 로 표시한다.
정점의 들어오는 연결성은 그 정점에서 들어오는 간선의 수이다.
정점 v의 들어오는 연결성은 𝒅𝒊n(𝒗) 혹은 |𝑵𝒊n(𝒗)| 로 표시한다.

실제 그래프의 연결성 분포는 두터운 꼬리 (Heavy Tail)을 갖는다.
즉, 연결성이 매우 높은 허브(Hub) 정점이 존재한다.

단, 랜덤 그래프의 연결성 분포는 높은 확률로 정규 분포를 갖는다.
연결성이 매우 높은 허브(Hub) 정점이 존재할 가능성이 0에 가깝다.

거대 연결 요소 (Giant Connected Component)

연결 요소 (Connected Component)는 다음 조건들을 만족하는 정점들의 집합이다.
연결 요소에 속하는 정점들은 경로로 연결될 수 있다.
위의 조건을 만족하며 정점을 추가할 수 없다.

{1,2,3,4}는 조건 1을 만족한다. 하지만 5를 더하면 조건 1이 여전히 만족한다.
{6,7,8,9}는 애초에 다른 연결 요소이다.
즉, 조건 2는 한 연결 요소 안에는 모든 원소들이 들어있어야 함을 의미한다.

거대 연결 요소는 대다수의 정점을 포함하는 연결 요소이다.
실제 그래프에는 거대 연결 요소가 존재한다.

랜덤 그래프에도 높은 확률로 거대 연결 요소가 존재한다.
단, 정점들의 평균 연결성이 1보다 충분히 커야 한다.

군집 구조

군집(Community)란 다음 조건들을 만족하는 정점들의 집합이다.

집합에 속하는 정점 사이에는 많은 간선들이 존재한다.
집합에 속하는 정점과 그렇지 않은 정점 사이에는 적은 수의 간선이 존재한다.

지역적 군집 계수 (Local Clustering Coefficient)는 한 정점에서 군집의 형성 정도를 측정한다.
정점 i의 지역적 군집 계수는 정점 i의 이웃 쌍 중 간선으로 직접 연결된 것의 비율이다.
이웃쌍 사이의 간선이 추가될 경우 지역적 군집 계수는 증가한다. (줄어들면 감소)
참고로 연결성이 0인 정점에서는 지역적 군집 계수가 정의되지 않는다.

1번 예시는 2, 3, 4, 5가 연결되어 있다. 그리고 각 이웃노드들은 1을 거쳐 다른 모든 노드로 갈 수 있다.
{2,1,3}, {2,1,4}, {2,1,5}, {3,1,4}, {3,1,5}, {4,1,5} = 6개
그러나 직접 연결된 노드들은 {2,3}, {2,4}, {3,5}, {3,5} 뿐이다. = 4개 => 4/6
2번 예시는 {2,1,3}, {2,1,4}, {2,1,5}, {3,1,4}, {3,1,5}, {4,1,5} => 6개
직접 연결된 노드들은 {2,3}, {2,4}, {3,5} => 3개 => 3/6
3번 예시는 이웃쌍들이 직접 연결되어 있지 않다.

정점 i의 지역적 군집 계수가 매우 높으면, 정점 i의 이웃들이 높은 확률로 서로 간선으로 연결되어 있음을 의미한다. 그렇다면 정점 i와 그 이웃들은 높은 확률로 군집을 형성한다.

전역 군집 계수 (Global Clustering Coefficient)는 전체 그래프에서 군집의 형성 정도를 측정한다.
즉, 전역 군집 계수는 각 정점에서의 지역적 군집 계수의 평균이다.
단, 지역적 군집 계수가 정의되지 않은 정점은 제외한다.

실제 그래프에서는 많은 군집이 존재해 군집 계수가 높다.
그 이유는 다음과 같다.

동질성 (Homophily) : 서로 유사한 정점끼리 간선으로 연결될 가능성이 높다.
전이성 (Transitivity) : 공통의 이웃이 매개 역할을 해줄 수 있다.

반면 랜덤 그래프는 지역적 혹은 전역 군집 계수가 높지 않다.
랜덤 그래프에서의 간선 연결이 독립적이기 때문에 공통 이웃의 존재 여부가 간선 연결 확률에 영향을 미치지 않기 때문이다.

군집 계수 및 지름 분석

다음 세 종류의 그래프의 구조를 분석

*작은 세상 그래프는 균일 그래프의 일부 간선을 임의로 선택한 간선으로 대체한 그래프

import networkx as nx #networkx import
import numpy as np
import matplotlib.pyplot as plt

#균일 그래프 로드
regular_graph = nx.Graph()
f = open('regular.txt', 'r')
for line in f :
    v1, v2 = map(int, line.split())
    regular_graph.add_edge(v1, v2)
f.close()

#작은 세상 그래프 로드
small_world_graph = nx.Graph()
f = open('small_world.txt', 'r')
for line in f :
    v1, v2 = map(int, line.split())
    small_world_graph.add_edge(v1, v2)
f.close()

#랜덤 그래프 로드
random_graph = nx.Graph()
f = open('random.txt', 'r')
for line in f :
    v1, v2 = map(int, line.split())
    random_graph.add_edge(v1, v2)
f.close()

#그래프 시각화
#정점의 위치 결정
pos = nx.spring_layout(regular_graph)
#정점의 색과 크기를 지정해 출력
im = nx.draw_networkx_nodes(regular_graph, pos, node_color = "red", node_size = 100)
#간선 출력
nx.draw_networkx_edges(regular_graph, pos)
#각 정점의 라벨 출력
nx.draw_networkx_labels(regular_graph, pos, font_size = 15, font_color = "black")
plt.show()

#정점의 위치 결정
pos = nx.spring_layout(small_world_graph)
#정점의 색과 크기를 지정해 출력
im = nx.draw_networkx_nodes(small_world_graph, pos, node_color = "red", node_size = 100)
#간선 출력
nx.draw_networkx_edges(small_world_graph, pos)
#각 정점의 라벨 출력
nx.draw_networkx_labels(small_world_graph, pos, font_size = 15, font_color = "black")
plt.show()

#정점의 위치 결정
pos = nx.spring_layout(random_graph)
#정점의 색과 크기를 지정해 출력
im = nx.draw_networkx_nodes(random_graph, pos, node_color = "red", node_size = 100)
#간선 출력
nx.draw_networkx_edges(random_graph, pos)
#각 정점의 라벨 출력
nx.draw_networkx_labels(random_graph, pos, font_size = 15, font_color = "black")
plt.show()


#전역 군집 계수 계산 함수
#지역 군집 계수의 평균
def getGraphAverageClusteringCoefficient(Graph) : 
    ccs = []
    #각 지역 군집 계수 계산 후 ccs에 추가
    for v in Graph.nodes :
        num_connected_pairs = 0
        for neighbor1 in Graph.neighbors(v) :
            for neighbor2 in Graph.neighbors(v) :
                if neighbor1 <= neighbor2 : continue
                if Graph.has_edge(neighbor1, neighbor2) :num_connected_pairs += 1
        #v 정점의 지역 군집 계수는 v 정점의 이웃들의 쌍의 수와 실제로 연결된 수를 계산홰야 함.
        cc = num_connected_pairs / ((Graph.degree(v) * (Graph.degree(v)-1)) / 2)
        ccs.append(cc)
    return sum(ccs) / len(ccs)


#지름 계산 함수
def getGraphDiameter(Graph) :
    diameter = 0
    for v in Graph.nodes :
        length = nx.single_source_shortest_path_length(Graph, v)
        max_length = max(length.values())
        if max_length > diameter : diameter = max_length
    return diameter


print('## Ragular Graph ##')
print('Graph Diameter : {0}, Average Clustering Coefficient : {1:.2f}'.format(getGraphDiameter(regular_graph), getGraphAverageClusteringCoefficient(regular_graph)))
print('## Small World Graph ##')
print('Graph Diameter : {0}, Average Clustering Coefficient : {1:.2f}'.format(getGraphDiameter(small_world_graph), getGraphAverageClusteringCoefficient(small_world_graph)))
print('## Random Graph ##')
print('Graph Diameter : {0}, Average Clustering Coefficient : {1:.2f}'.format(getGraphDiameter(random_graph), getGraphAverageClusteringCoefficient(random_graph)))

피어세션 회의 내용

해야할 일

1. 그래프란 무엇이고 왜 중요할까?

그래프는 정점 집합과 간선 집합으로 이루어진 수학적 구조입니다
그래프는 복잡계를 표현하고 분석하기 위한 언어입니다

2. 그래프 관련 인공지능 문제

정점 분류, 연결 예측, 추천, 군집 분석, 랭킹, 정보 검색, 정보 전파, 바이럴 마케팅 등

3. 그래프 관련 필수 기초 개념

방향성이 있는/없는 그래프, 가중치가 있는/없는 그래프, 동종/이종 그래프
나가는/들어가는 이웃

4. (실습) 그래프의 표현 및 저장

파이썬 라이브러리 NetworkX
간선 리스트, 인접 리스트, 인접 행렬

실제 그래프 vs 랜덤 그래프: 실제 그래프는 복잡계로부터 얻어지는 반면, 랜덤 그래프는 확률적 과정을 통해 생성합니다
작은 세상 효과: 실제 그래프의 정점들은 가깝게 연결되어 있습니다
연결성의 두터운 꼬리 분포: 실제 그래프에는 연결성이 매우 높은 허브 정점이 존재합니다
거대 연결 요소: 실제 그래프에는 대부분의 정점을 포함하는 거대 연결 요소가 존재합니다
군집 구조: 실제 그래프에는 군집이 존재하며, 실제 그래프는 군집 계수가 높습니다
(실습) 파이썬을 이용한 지름 및 군집 계수 분석

그래프는 인접 리스트 방식과 인접 행렬 방식으로 표현할 수 있습니다.

인접 리스트 방식이란 그래프의 한 정점에서 나가는 이웃들과 들어오는 이웃들을 저장하는 방식으로 메모리 사용량을 줄일 수 있습니다. 하지만, 간선을 탐색할 때 모든 이웃들을 검색해야하는 단점이 있습니다.

반대로 인접 행렬 방식은 그래프를 (정점 수) × (정점 수) 크기의 행렬로 나타내며 행렬 i행 j열의 원소에 대해서 정점 i
와 j 사이에 간선이 있으면 1, 없으면 0 로 표현합니다.

이 방식은 간선을 탐색할 때 행렬 indexing으로 바로 접근할 수 있지만, (정점 수) × (정점 수)의 메모리를 사용하는 단점이 있습니다.

트랜스포머 복습

123okk2.tistory.com/164

728x90

저작자표시 비영리 변경금지

'BOOSTCAMP AI TECH > 5주차_Machine Learning with Graphs' 카테고리의 다른 글

[BOOSTCAMP AI TECH] 25일차_ GNN (0)	2021.02.26
[BOOSTCAMP AI TECH] 24일차_정점 표현 & 추천 시스템 (심화) (0)	2021.02.25
[BOOSTCAMP AI TECH] 23일차_군집 탑색 & 추천 시스템 (0)	2021.02.24
[BOOSTCAMP AI TECH] 22일차_페이지랭크 & 전파 모델 (0)	2021.02.23